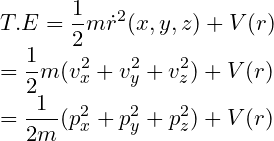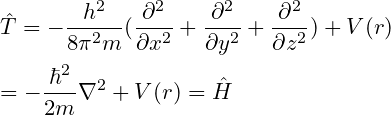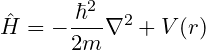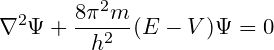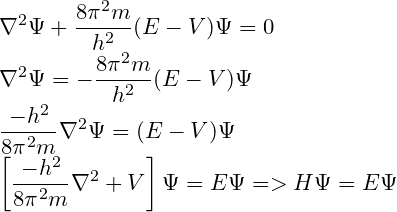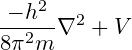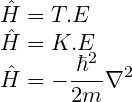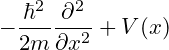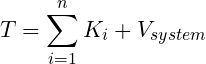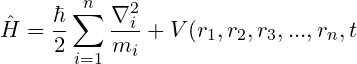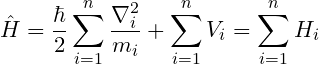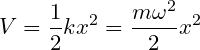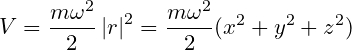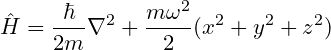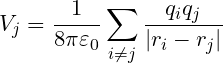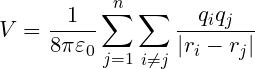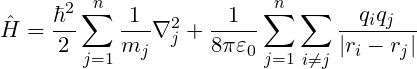When you study quantum mechanics, there you have to work with different operators. So, here we will discuss in-depth the Hamiltonian Operator(H) which we call Total Energy Operator(H).
Here we know that according to classical mechanics, the total energy(T) of a system of a particle will be the sum of the kinetic energy(K) and the potential energy(U) of that system.
This total energy is called the Hamiltonian operator in quantum mechanics.
Before discussing the Hamiltonian in-depth, we will learn about the operator. You should also know how the equations of classical mechanics are written in quantum mechanics.
As a result, you will have no problem understanding the various applications of this operator.
Observable and Operators in Quantum mechanics
1. Observable is the properties of a system that you can measure. Such as mass, distance, displacement, work-energy, etc.
2. In order to measure the properties of observable, you need to perform some field operations. This operation is represented by the operator.
Suppose here you are asked to do a density measurement of a system. In this case, you need to divide the mass(M) by volume(V) to determine the density(D).
So, you notice that the mass(M) and volume(V) here are observable or operand. And the division(-) is the operator.
Notice in this table below that the operator has been identified with different examples here.
Classical mechanics equation in Quantum mechanics
Due to the failure of classical mechanics, Newtonian mechanics took on a new form in quantum mechanics. In other words, the whole concept of classical mechanics has changed to quantum mechanics.
Classical mechanics can never describe the movement of particles with small mass and high-speed velocity. Here you have to work with the theory of relativity or quantum mechanics.
In this case, every concept of classical mechanics will remain the same but the equation of motion will change.
1. Displacement
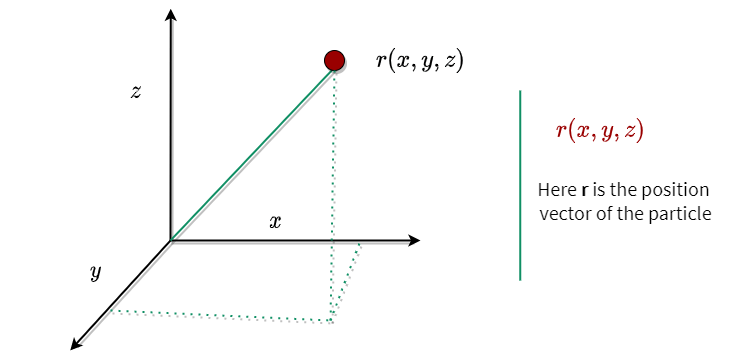
Displacement is the minimum distance between the final state and the first state of a moving particle. Displacement here is always a vector quantity that has a specified value and direction.
In both quantum mechanics and classical mechanics, we define displacement by position vectors.
2. Momentum
Momentum is used to sense the amount of force applied to a moving object. With the help of Momentum, you can know the nature of the applied force on an object.
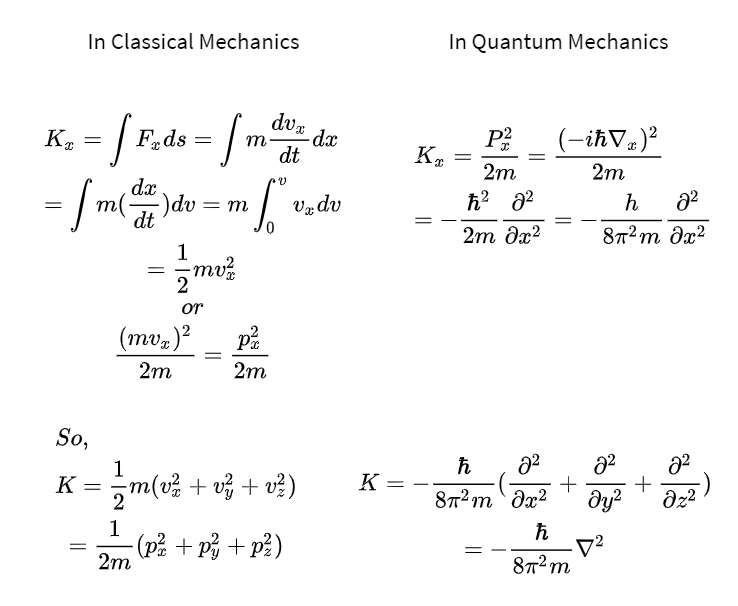
Momentum is usually represented by the product of the mass and velocity of a moving object. But in this case of quantum mechanics, the equation of momentum will be different.
3. Kinetic Energy
The amount of energy that an object gains due to its motion are called kinetic energy.
4. Potential Energy
In a force field, the amount of energy that an object gains to change its position is called potential energy. Potential energy is denoted by $V(x)$ in both cases.
Hamiltonian operator
Suppose a particle is moving in three-dimensional space. Then, this will be the total energy of the particle
If the particle is too small and its velocity is too high then you cannot apply the rule of classical mechanics there. Here you need to use quantum mechanics.
So, according to quantum mechanics, the total energy of that particle will be
Thus, the Hamiltonian operator of a particle in three-dimensional space will be
Hamiltonian operator from schrödinger equation
We will prove this operator with the new form of the schrödinger equation.
Here we will modify the schrödinger equation and convert it to a new form. Thus, the schrödinger equation is
Here ψ is the wave function and V is the potential energy.
We know that total energy(E) is always equal to that of Hamiltonian operators.
So, we will try to put the total energy in the schrödinger equation on one side. Then the hamiltonian will come out automatically.
Thus, the value of $ \hat{H}$ from the schrödinger equation will be
Hamiltonian operator of free Particle
Free particles are those particles on which the total applied force is zero. That is, the particle may move in free space at an equal velocity or no force field exists on it.
Since the total force on the particle will be zero, thus, the potential energy of the free particle is always assumed to be zero.
That is, the total energy of the free particle will be the kinetic energy due to the motion of that particle.
Hamiltonian for one Dimensional
When a particle moves over a straight line, the value of ∇ changes. In that case, the value of the this operator will be
Hamiltonian for N particles System
Suppose an N particle system is taken here, in which nth particles are present. This system can have two conditions.
1. First condition is that the particles may interact with each other. In this case, each particle will have its own potential energy and with it will also have mutual potential energy.
Thus, the system will have total energy
Then the Hamiltonian of that system will be
2. Second condition is that each particle in the system is located independently. That is, each particle in the system will have independent potential energy in which case the system will not have mutual potential energy.
Thus, in this case, the Hamiltonian of the system would be
Hamiltonian operator for Simple Harmonic Oscillator
The potential energy of any particle due to simple harmonic oscillator will be
If you imagine three dimensional space then the potential energy of a particle will be
Thus, the simple harmonic oscillator will cause the Hamiltonian of any particle to be
Hamiltonian operator for charge particle
Suppose $q_{1}$ and $q_{2}$ are the two charge particles taken and the distance between them is kept r. The potential energy of $q_{1}$ for $q_{2}$ will be
When you take $N$ charge particles, the total potential energy of the $q_{j}$ charge particle due to N-1 charged particle will be
Then the total potential energy of the whole system with N charge particles will be
Thus, the Hamiltonian of the whole charge system will be