What is a System of Particles?

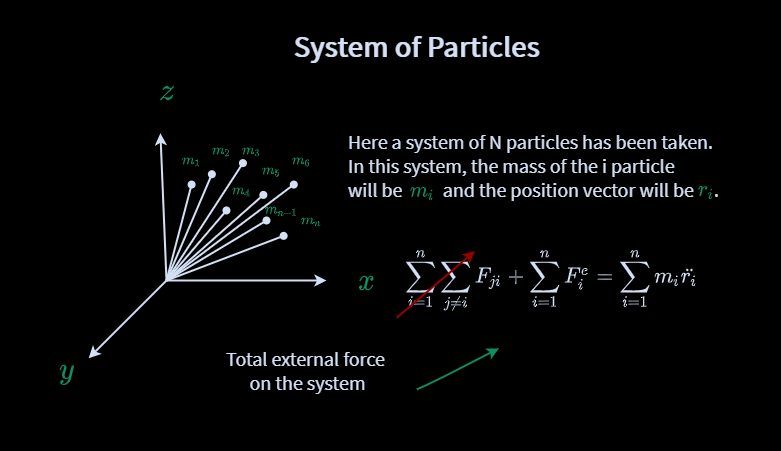
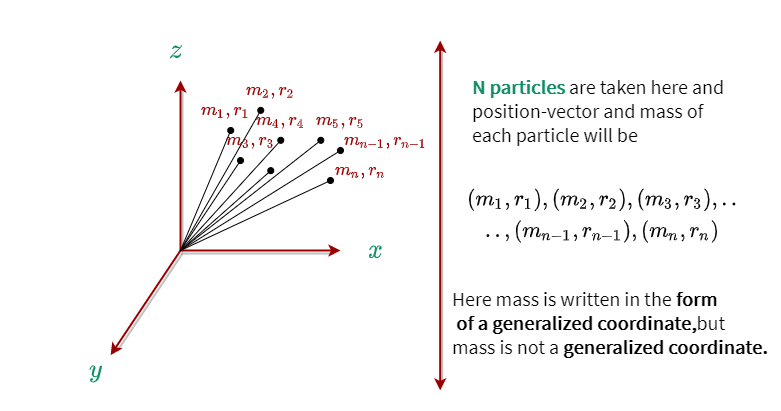
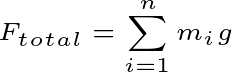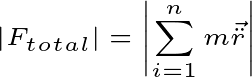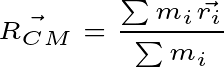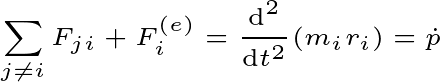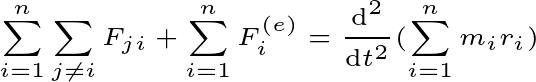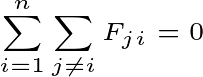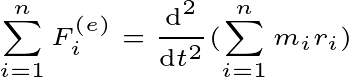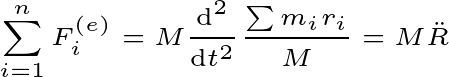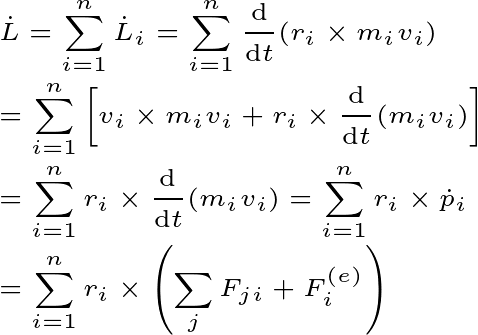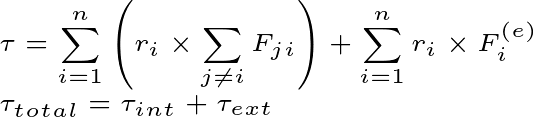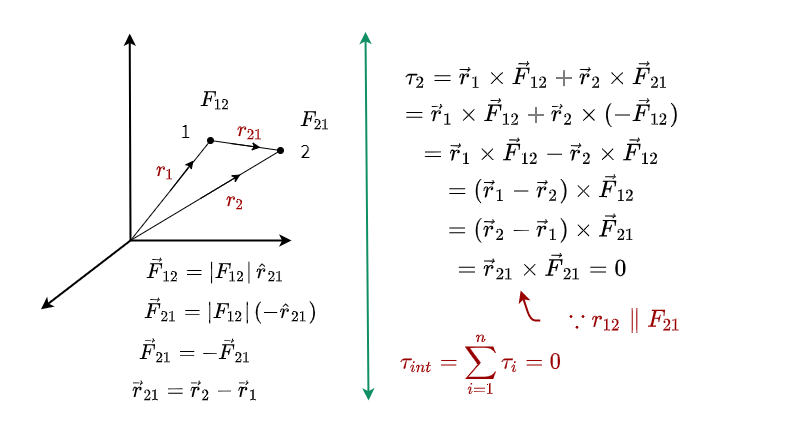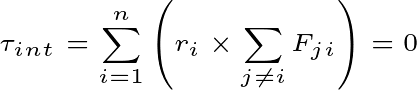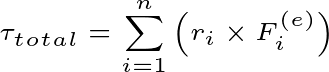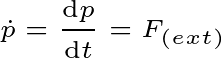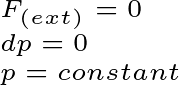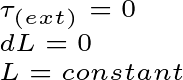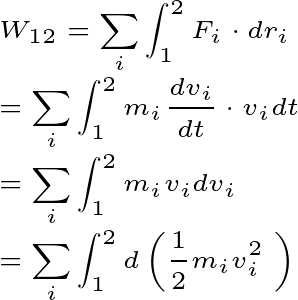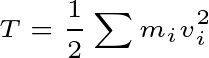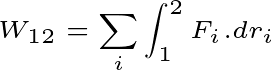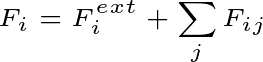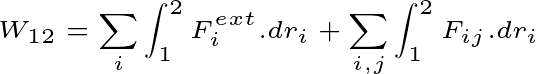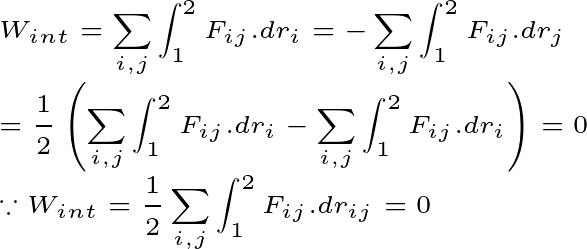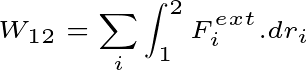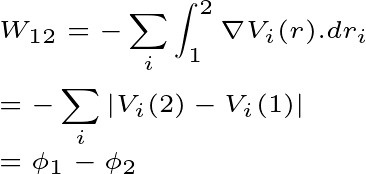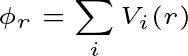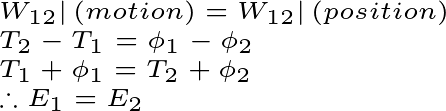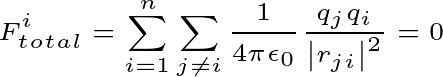Simply put, in mechanics, the system of particles is the sum of more than one specified particle. So, look at this figure below

Here we have taken N particles. And the mass of ith particle will be m_i and the position vector will be r_i.

Why systems are needed in Physics?

When you read physics, you will hear the word ‘system’ many times. Many of you may have a question in your mind as to why more than one object or particle in physics is considered a system!

We took n particles according to the question. And suppose, every particle is under gravity. In that case, you don’t have to use any system to calculate the force. Because you know the value and direction of the applied force on each particle. In this case, you can easily calculate the total force

Suppose you place these particles in an external force field where the value of the applied force depends on the position vector of the particle. In that case, it will not be easy to find the value of the total force by finding the value of the individual force of each particle.

Because force is a vector quantity. And in this case, the direction of the force of each individual particle will be different. So, there will be a total applied force on N particles …

Thus, it is impossible to calculate the force by considering each particle independently from the above equation. In this case, you have to treat the particles as a system.

You need to remember that there is a point in the system where all the mass of the system is centered. Which we know as the center of mass. That is, if you apply a force at this point, the linear motion of the system will be created.

Thus, applying force on an individual particle will change the motion in the same way that applying force on a center of mass will change the motion of the system.

For this, the aggregate of more than one particle is always considered as the system of particles.

Generalized Coordinate of Systems of Particles

The minimum number of independent coordinates required to describe the configuration of a dynamic system at any given time is called generalized coordinates of that system.

For example, a particle is moving in a plane. In this case, you need to use a minimum of two coordinates(x,y) to know the configuration of the particle. Even if you use polar coordinates, you have to use a minimum of two coordinates(r,θ).

Suppose you take a dynamic system of N particles, in which case you will need a minimum of 3N generalized coordinators to describe the configuration of the system.

When you apply constraints or constraints force on the system of particles, the generalized coordinates of the system will not be 3n. In this case, the value of the independent coordinates of the system will be reduced.

If the constraints above the system are k, then the system will have total generalized coordinates

For example, suppose a constraint is applied to a system so that every particle in the system will move on the surface of the sphere. In that case, the system will have generalized coordinates f_k=2N( ∴ f=N ).

Because when the particle moves on the surface, there will be constraint equation

In this case, the total coordinates are three, but here the total minimum independent coordinates for each particle are two because the value of Z(\[\left | z \right |=\sqrt{r^{2}-x^{2}-y^{2}}\]) depends on the other two coordinates. Then the total coordinate for the N particle will be 2N where the constraint will be N.

There is a question among many as to how the Cartesian coordinates are written in the form of generalized coordinates.

You see, the Cartesian coordinate is always written in the form (x,y,z), just like the generalized coordinate is always written in the form of q_i.

If the total generalized coordinates of a dynamic system are f then the cartesian coordinates of that system will be

External force and torque on the Systems of Particles

When external force and torque are applied to a group of particles, three types of motion can be generated in this system.

1. If a force is applied to the center of mass of a system, the system will generate linear motion.

2. Rotational motion occurs when pure torque is applied to a system. Here pure torque means that the total external force will be zero i.e. the system will not have any linear motion.

3. Mix motion will occur when both external torque and force are applied to a system.

So, below we will discuss the causes of these three types of motion.

1. External force

Suppose N particles are present in the system. According to Newton’s second law, there will be a total force on the ith particle

Since there are many particles stored in this system. The internal force will work among them. There will be a total internal force on the ith particle $\sum F_{ji} $.

In the case of N particles, there will be an equation of system motion

You know, according to Newton’s third law, every action has the opposite reaction. That is, the total internal force between the two particles will be zero. Then in the case of N particles, the total internal will be zero.

Then the external force will be the only reason for the motion of the system.

And you can write this equation as the center of mass of the system.

Here M is the total mass of the system $M=\sum m_{i}$

2. External torque

Now, the angular momentum of the ith particle will be

Then the total torque of the whole system will be

So, here the sum of torque by internal force and external force will be equal to the total torque of the group of particles.

Total torque of the system will be zero by internal force. So, take a look at this figure below then you will understand how the total torque is being zeroed by the internal force.

 

Here, two particles are taken to explain to you. And the position vectors of the two particles are r₁ and r₂. The internal forces between the two particles are F₁₂ and F₂₁ which are opposite and equal to each other. And the displacement vector between the two particles is r₂₁.

If you look at the picture above, you can see that the total torque between the two particles will be equal to the cross product of displacement vector and internal force. And the displacement vector and the internal force are parallel to this system. That is, the cross product will be zero. That is, the total torque of the two-particle systems is zero.

Then we can say that the total torque of a system with N particles by internal force will be zero.

That is, the total torque of the system will be equal to the total torque by the external force.

Conservation momentum of a system

We can sense the amount of external force and torque applied to an object by looking at the momentum. Generally, the momentum of a system will be conservative when the value of total external force and torque applied to the system is zero.

1. Conservation of linear momentum

The total external force on a system is equal to the rate of change of momentum with respect to time. So, we can write

If the value of external force is zero then there will be no change in momentum. That is, there will be a momentum constant. And this is the conservation of linear momentum. So, notice below that if the change of momentum is zero then the value of momentum will always be constant.

2. Conservative angular momentum

Similarly, if the total torque on a system is zero then the angular momentum of that system will always be constant.

That is, the system will continue to rotate with an equal angular velocity(ω).

Kinetic Energy and Potential Energy of a System of Particles

When a system is in motion or changes position, the system gains some kind of energy. If the system is located in the conservation force field then the total energy of the system will always be constant.

1. Kinetic energy

The amount of energy that is gained for the dynamic state of a system is called the kinetic energy of that system.

Suppose there is a system of mass moving from point 1 to point 2. And m external force on the system is being applied. Then the total work done of the system will be

Therefore, the total Work done of the system will be

Here T is the total energy of the system in the particular position

If you look at this equation above, kinetic energy (T)will never be negative at any one point. However, changes in kinetic energy can be negative.

2. Potential energy

The amount of energy that a system gains or loses to change its position is called the potential energy of that system.

We know that there will be a total force on the ith particles of the system

Thus, total work done of the system will be equal to the potential energy of external force and internal force.

The potential energy of the system will be zero by the internal force. So, look at this proof below

So, the total potential energy of the system here will depend entirely on the external force.

Suppose a conservation force field is taken here. And the particle is moved from point 1 to point 2. In this case, there would be a total applied force on the particle $F=-\nabla V$. Here v is the potential of the conservation force field. then

Here Φ_r is the total potential energy of the system in a given position. And r is the position of the system.

Conservation energy of the system of particles

When the system is in the conservation force field, the system has total energy constant. That is, Work done will be equal in both cases when the system remains dynamic and changes position.

Finally, when a system or particle moves within the conservation force field, it has total energy constant at every moment. That is, as the kinetic energy of the system increases, the potential energy decreases, and as the potential energy increases, the kinetic energy decreases.

Question and answer

Here are some standard problems discussed so that your concept will be clearer in a more beautiful way.

Problem1 Suppose you take a system of n charged particles. So, what is the total internal force of the system in that case?

When an electrostatic force with equal and opposite directions is applied between two charged particles, it is an internal force. If you think of these two particles as a system, then the total force of the system will be zero. Then the total internal electrostatic force will be zero even in the case of n particles.

Problem2 What will be the total potential energy in the case of N charged particles?

If you look at the jth particle, then the total potential energy will be due to the N-1 charge particle.