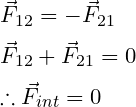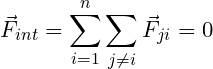When more than one particle is discussed in physics, the sum of those particles is considered a system.
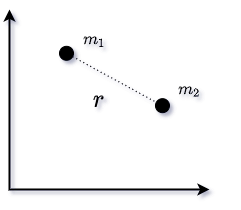
Here we will take a two-particle system according to the given concept. Whose mass is \(m_1\) and \(m_2\). And the distance between them is \(r\).
When you consider a system of more than one particle, you need to know the center of mass of the system. Because the center of mass is a point where all the masses of the system are supposed to be centered.
As a result, you can easily solve the dynamic condition of the system mathematically.
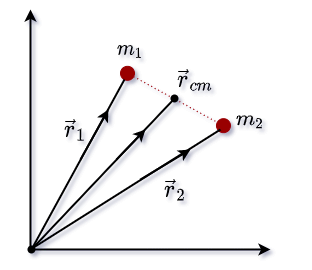
Suppose here N individual particles are taken and the mass of the \(i th\) particle is \(m_i\) and the position vector is \(r_i\). Then the center of mass of the system will be
\[ \vec{r}_{cm} = \frac{\sum m_i\vec{r}_i}{\sum m_i} \]
Position vector of center of mass for two particles
And here two particles are considered whose mass and position vectors are\((m_1,\vec{r}_1)\) and \((m_2,\vec{r}_2)\). and you notice the figure below
In this case, the center of mass of the system will be located on the connected straight line between the two particles. Then the position vector of the center of mass will be
\[ \vec{r}_{cm} = \frac{ m_1\vec{r}_1 + m_2\vec{r}_2}{m_1+m_2} \]
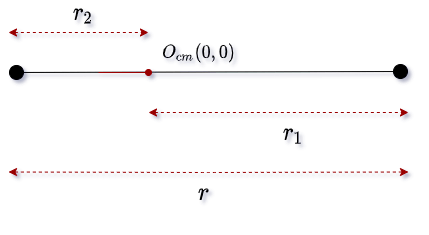
If the center of mass is located at the origin of the coordinate, then the position vector will be a null vector. That is
$$ \vec{r}_{cm} = \vec{0} $$$$ \frac{ m_1\vec{r}_1 + m_2\vec{r}_2}{m_1+m_2} = \vec{0} $$
$$ m_1\vec{r}_1 + m_2\vec{r}_2 = \vec{0} $$
$$ \therefore m_1\vec{r}_1 = m_2(-\vec{r}_2) $$
You can see in the image below that r2 is located on the opposite side of the origin. For this reason, r2 is negative here.
Velocity of center of mass
Suppose two particles are moving, then the center of mass will also move due to their mobility. And the center of mass will have a specific velocity.
If you differentiate the position vector in respect of time, you will get the velocity of the center of mass.
$$\vec{\dot{r}}_{cm}=\frac{m_1\vec{\dot{r}}_1+m_2\vec{\dot{r}}_2}{m_1+m_2}$$
$$\vec{v}_{cm}=\frac{m_1\vec{v}_1+m_2\vec{v}_2}{m_1+m_2}$$
Here vcm is the velocity of the center of mass, v1 and v2 are the velocities of both particles.
Acceleration of COM
When the position vector of COM is double derivative in respect of time, it represents the total acceleration of the system.
$$\vec{\ddot{r}}_{cm}=\frac{m_1\vec{\ddot{r}}_1+m_2\vec{\ddot{r}}_2}{m_1+m_2}$$
$$\vec{a}_{cm}=\frac{m_1\vec{a}_1+m_2\vec{a}_2}{m_1+m_2}$$
Here acm is the acceleration of the center of mass, a1 and a2 is the acceleration of the two individual particles.
Force on the system
When you will discuss the motion of more than one individual particle. In that case, two types of forces will work in the system.
- External Force
- Internal Force
1. External Force
External force is the type of force that is applied to the system from the outside. And this external force will be equal to the rate of change of the momentum of the system.
Then according to Newton’s second law the total external force will be
$$\vec{F}_{ext}=\frac{\mathrm{d} }{\mathrm{d} t}\left ( m_1\vec{v}_1 + m_2\vec{v}_2 \right )$$
And if the mass of the system is constant then the external force will be equal to the product of mass and acceleration of the system.
In this case, the acceleration of the system will be equal to the acceleration of the center of mass. And the total mass will be m1+m2. Then total external force will be
$$\vec{F}_{cm}=\left ( m_1 + m_2 \right )\vec{a}_{cm}$$
$$\vec{F}_{ext}=m_2\vec{a}_{1} + m_1\vec{a}_{2}$$
$$\vec{F}_{cm}=\vec{F}_{ext}$$
Suppose here if N particles are taken. Thus the product of the total mass of a system and the vector acceleration(acm) of the center of mass is equal to the vector sum of all the external forces acting on the individual N particles of the system.
$$a_{cm}\sum m_i = \sum_{i=1}^{n} m_ia_i $$
$$\therefore a_{cm}=\cfrac{\sum\limits_{i=1}^{n} m_ia_i}{\sum\limits m_i}$$
When no external force acts on the system
$$\sum_{i=1}^{n} \vec{F}_{i} = 0$$
$$\vec{a}_{cm}=0$$
$$\therefore \vec{a}_{cm} = constant$$
If the external force on the system is not applied, the acceleration of the center of mass will be zero and the velocity will be a constant vector.
2. Internal Force
The internal force on a particle depends on its physical properties. When more than one charged particle is taken, the Coulomb force acts between them.
Also, the gravitational force acts between them when more than one tiny massive particle is taken.
In exactly the same way the gravitational force will work between two particles which will equal and act in opposite directions to each other.
If you calculate the total gravitational force in the case of these two particles, you will see that the total force will be zero.
In exactly the same way if n particles are taken. Then the total internal force of the system will be a zero vector.