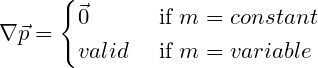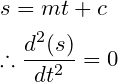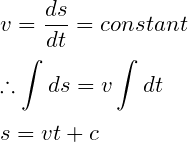Hey, Physics Thinker In this tutorial we will discuss an important concept which is Zero Acceleration. You need to understand what effect a particle has on its motion when it moves at zero acceleration.
Before reading this tutorial, we have an important request for you to always try to feel every concept of physics practically. Which will increase your interest in physics.
What is Zero Acceleration?
According to the definition, the rate of increase of velocity is called acceleration.
You just imagine that if the rate of increase of velocity is zeroed out, that is, if an object moves at constant velocity, its acceleration will be zero.
\[|\vec{a}|=\left| {\frac{d(\vec{v})}{dt}} \right| = 0\]
Since acceleration is a vector quantity, acceleration must always be expressed in the form of a zero vector.
That is, you don’t have to just write zero here, you have to indicate with an arrow above zero. And this is the rule for writing zero vectors. For example
$$\vec{a}=\vec{0}$$
Theoretically, when a particle moves in constant velocity, there is no change in velocity with time. Then its acceleration is called zero acceleration.
Mathematically, since velocity is constant then the first time derivative of velocity will be zero which indicates the acceleration of a moving object.
$$\vec{v}=constant$$$$\therefore \left\lvert\frac{d(\vec{v})}{dt}\right\rvert = \vec{0}$$
Impact on Motion
Since the total acceleration of any moving particle is zero. Then the total applied force on the particle will be zero.
According to Newton’s first law, if the total applied force on a moving particle is zero, then the particle is along a straight line with constant velocity.
In the case of zero acceleration, the direction of motion of the particle will not change. And if the direction of motion changes then the velocity of the particle will not be constant.
Impact on Velocity
You understand that the velocity of a particle will be constant for zero acceleration. That is, there will be no change in the value and direction of velocity over time.
Mathematically, if we express the value of velocity, we can see that velocity becomes a constant value. Notice the following equation
$$\therefore \left\lvert\frac{d(\left|\vec{v}\right|)}{dt}\right\rvert = 0$$
$$\left|\vec{v}\right|=constant$$
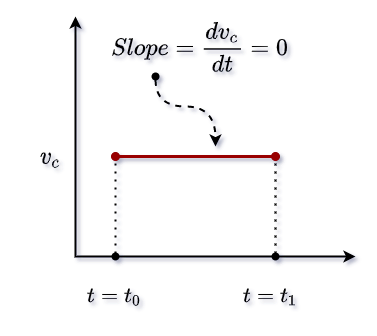
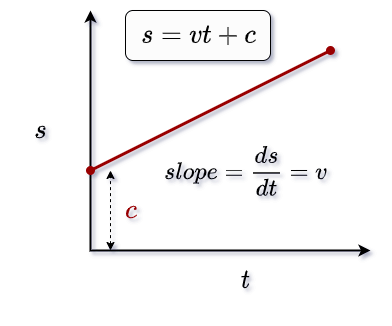
Graphically, since velocity is constant over time, the v-t graph will represent a straight line parallel to the time axis.
And the slope of velocity and time graphs will always represent acceleration. If you look at the image above, the slope will be zero.
Impact on Force
Based on this concept many may think that the force of any system will always be zero, but no.
Because force does not mean the product of mass and acceleration. You can use this concept where the mass of the system or particle is always constant.
According to Newton’s second law of motion, the total applied force on a system or particle will be equal to the rate of change of momentum.
1. Constant Mass
In this case, the mass of the system is kept constant. Then the total force of the system will be equal to the product of mass and acceleration.
You always use this equation. Since the mass of the system is constant, that is, if the acceleration is zero, the total applied force on the system will be zero. Notice the following calculation
2. Variable Mass
In fact, there are many systems whose mass changes with the speed of the system. This type of system is called a variable mass system. Such as gas balloons, rockets, etc.
Thus, the total applied force on this type of system is not just equal to the product of mass and acceleration. Rather, the total applied force also depends on the variable mass.
In this case, even if the total acceleration of the system is zero, the total force of the system for the variable mass will not be zero.
Questions and Answers
1. In the case of zero acceleration, will the change of momentum always be zero?
No, in the case of constant mass the change in momentum of the particle will always be zero. However, when the mass of the system is variable, the change of momentum will not be zero.
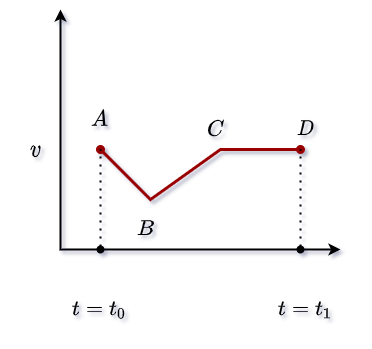
2. Below you are given a velocity and time graph. You look at this graph and tell where the particle acceleration will be zero?
The slope of velocity and time graph always refers to acceleration. Then you need to find the point or duration in the graph where the value of slope will be zero. Then we can say that the value of acceleration at that point or duration is zero.
If you look at the graph, you will see that the value of slope at point B and CD duration is zero. Then the value of acceleration at B point and CD duration will also be zero.
3. What will be the relation between time and displacement in the case of zero acceleration?
Mathematically, the double-time derivative of displacement always represents acceleration.
Then you have to make the relation of time with the displacement whose double time derivative will be zero.
Here m is the constant velocity. And you could prove the relationship between this displacement and time in the opposite way.
In this case, velocity is constant. So if you integrate velocity into the respect of time, a relation will be created between displacement and time which will represent zero acceleration. So, look at this calculation below
So, if you draw a graph based on this equation, it will be a graph
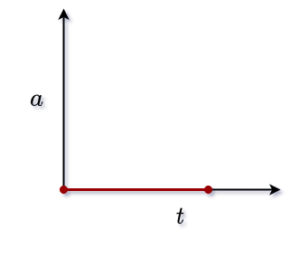
4. A simple question is what will be the acceleration and time graph?
In this case, the value of acceleration is zero. That is, the value of acceleration will remain zero as time goes on.
When a particle moves uniform velocity, its acceleration will be zero. That is, the velocity of a moving particle will not change as it increases over time
Conclusion
Many students have misconceptions about this concept. Of course, it has been discussed in depth so that you do not have any difficulty in understanding.
I hope you understand the impact of acceleration on other dynamic physical quantities.
