This tutorial discusses important conceptual examples of distance. And the answer is given with the example. So, you will have no difficulty in understanding.
If displacement of a particle is zero, then distance will be
- must be zero
- may or may not be zero
- cannot be zero
- depends upon the particle
Explanation
may or may not be zero
If displacement of a particle is zero, then distance may or may not be zero.
In both cases, displacement of any particle will be zero.
1st case: When a particle is stationary, both displacement and distance will be zero.
2nd case: A particle will keep moving. But, initial point and final point are same. In that case, displacement of particle is zero but distance is not zero.
If distance covered is zero, then displacement will be
- depends upon particle
- cannot be zero
- may or may not be zero
- must be zero
Explanation
Distance zero means particle is stationary. That is, in this case, the displacement of a particle must be zero.
If a particle covers a minimum distance, then the relationship between distance(d) and displacement(s) will be
- d equal to s
- d less than s
- d greater than s
- None
Explanation
Minimum distance between two points will be equal to linear distance between two points.
By definition, the linear distance between two points is called displacement. Thus, in this case, distance and displacement will be equal.
If a particle moves in a curved path. In that case, what will be the relation between distance(d) and displacement(s) of a particle?
- \(d = s\)
- d > s
- d﹤s
- None
Explanation
d > s
When a particle moves along a curved path, the distance will always be greater than the displacement. Because displacement is the linear distance between two points.
Suppose, you move from point a to point b along a semicircle path. Then, what will be your displacement and distance?
- r and 2πr
- r and πr
- 2r and 2πr
- 2r and πr
Explanation
If a particle moves along a semicircular path from point A to point B, the distance traveled by the particle will be πr.
If the distance of particle is πr then the displacement of particle will be equal to diameter of the semicircle.
Ratio of displacement and distance traveled by an object can never be
- equal to 1
- less than 1
- greater than 1
- zero
Explanation
Displacement will be equal to or smaller than distance, but not larger. For this reason the ratio of displacement and distance will not be greater than 1.
A runner completes one round of a circular path of radius r in 40 seconds. His displacement and distance after 2 minutes 20 seconds will be
- zero and 5πr
- 2r and 2πr
- 2r and 7πr
- 2r and 5πr
Explanation
If the runner completes one round in 40 seconds, he will complete two and a half rounds in 2 minutes and 20 seconds.
You know, moving from initial point back to initial point, Displacement will always be zero.
Thus, the runner’s displacement will be zero for the complete two rounds. However, for rest of the half round, runner’s displacement will be equal to diameter of circular path.
s = 2r
And the runner’s total distance cover will be
d= (2+1/2)×2pr = 5pr
Equation of motion of an object in two-dimensional space is, x = 5t² + 2; y = 2t² + 5. Motion path of the object is
- Circular
- Stright line
- Hypothetical
- Elliptical
Explanation
According to the question, x = 5t² + 2, y = 2t² + 5.
You put the value of t² in the equation of y.
So, you look at the equation above, it’s a straight line equation. Then this moving particle will move along a straight line.
A body covered a distance of L m along a curved path of a quarter circle. The ratio of distance to displacement is
- π/2√2
- 2√2/π
- π/√2
- √2/π
Explanation
As shown in the figure above, suppose the radius of the quarter circle is r.
Then total distance will be
And displacement will be
s=√2r
Therefore, the ratio of displacement to distance is π/2√2.
A car running at a speed of 18 km/h, the distance covered in 3s is
- 4m
- 5m
- 10m
- 15m
Explanation
Above question gives the value of speed and time. However, Units of speed and time are defined in two different ways.
Thus, the unit of speed has to be converted in the same method according to the unit of time and answer. Here the unit of time and answer is given in the SI method.
v = 18 ×1000 /3600 = 5 m.s-1
Therefore, in three seconds the distance of car will be
d = vt = 15 m
Two bodies of different masses ma and mb are dropped from two different heights, viz a and b. Ratio of times taken by the two to drop through these distances is
- a : b
- ma/mb : b/a
- √a : √b
- a2 : b2
Explanation
You know when an object is dropped from top to bottom. In that case, Total time will take t seconds. t will be equal to
Notice equation above, time does not depend on mass of the object. So, for a and b heights, the total time taken is
Therefore, the ratio will be two different times
Equation of velocity of an object v = at. Distance that particle travels in first 6s is
- 8a
- 10a
- 16a
- 18a
Explanation
When a particle moves along a straight line. Then, if the velocity is integrated in the respect of time, it will represent the total distance traveled by the particle.
According to the question, if v = at, then the total distance between the first six seconds will be
An object gains v velocity after crossing a distance h when it falls freely from a rest on the gravitational surface. And how far will the velocity be 2v if the object travels?
- 4h
- 6h
- 8h
- 10h
Explanation
When the speed of the object is v then the object covers h distance. And since the object was dropped from rest, its initial velocity will be zero.v² = 2gh
Assuming that the object gains 2v speed then its distance is h’.
(2v)² = 2gh’
h’ = 4h [ v² = 2gh ]
A body starting from rest and has uniform acceleration 8 m/sec2. The distance traveled by it in 6th second will be
- 32m
- 44m
- 56m
- 70m
Explanation
If an object moves along a linear path with a acceleration, the total distance in the nth second will be
Sn = u + ½(2n-1)
Then according to the question, in the 6th second the distance of the object will be
S6 = ½ × 8 × 11 [ u =0]
∴ S6 = 44
A body starts from rest, the ratio of distances traveled by the body during the 5th and 6th seconds is
- 7 : 5
- 5 : 7
- 9 : 5
- 9 : 11
Explanation
Like question number 14, the distance that the object will cover in the 5th and 6th seconds is
S5 = ½ × a × 9
S6 = ½ × a × 11
Thus, the ratio between the two distances will be S5 : S6 = 9 : 11
Distance traveled by a particle starting from rest and moving with an acceleration 4/3 m/s2 in the third second is
- 5m
- 6m
- 10/3m
- 20/3m
Explanation
A particle is moving at a acceleration 5m/s² from rest. Then the initial velocity of the particle is zero.
S3 = ½ × 4/3 × (6-1) [u =0]
∴ S3 = 10/3m
Initial velocity of a particle is 10 m/sec and its retardation is 2 m/sec2. The distance covered in the fifth second of the motion will be<
- 1m
- 19m
- 50m
- 59m
Explanation
If the particle has initial velocity. In that case, the total distance of the particle in the nth second will beSn = u + ½a(2n-1)
According to the question, u =10 m/s and a = – 2 m/s², than
S5 = 10 – ½×2×9
∴ S5 = 1
A particle moves with constant acceleration for 6 seconds after starting from rest. The distance traveled during the consecutive 2 seconds interval are in the ratio
- 1 : 1 : 1
- 1 : 2 : 3
- 1 : 3 : 5
- 1 : 5 : 9
Explanation
At intervals of two seconds, the distance of the object in nth second will beSn = 2u + 2a(n-1)
Then, the distance covered in 2nd, 4th and 6th seconds will be
S2 = 2a(n-1) = 2a(2-1) = 2a
S4 = 2a(n-1) = 2a(4-1) = 6a
S6 = 2a(n-1) = 2a(6-1) = 10a
∴ S2 : S4 : S6 = 1 : 3 : 5
A particle moves on a straight line and velocity varies with time as v = 4t, find the distance traveled by the particle in the interval of 2 s to 4s
- 12m
- 24m
- 36m
- 48m
Explanation
In this case, to find the total distance, you have to integrate at intervals of two to four
If a particle travels from rest at uniform acceleration and crosses the x path in first 2 s and the y path in next 2 s, then which of the following is correct?
- y = 3x
- y = 2x
- y = x
- y = 4x
Explanation
If the particle crossed x distance in first two seconds and y distance in second two seconds, then the particle crossed total x + y distance in four seconds. If the particle has moved from a rest. Then we can write that,
A rock is falling freely under the influence of gravity. h1, h2, and h3 distances cross at intervals of the first, second and third 5s of the fall period. Then the relationship between h1, h2 and h3 will be
- h1 = h2/3 = h3/5
- h2 = 3h1 and h3 = h2
- h1 = h2 = h3
- h1 = 2h2 = 3h3
Explanation
In this case, the stone covers three distances in 15 seconds at an interval of five seconds. At a five second interval, the total distance in nth second will be
An object starts its journey from rest at constant acceleration and crosses the x distance in first 10s and the y distance in next 20s. The relationship between x and y is
- y = 7x
- y = 5x
- y = 8x
- y = 9x
Explanation
This question is like mcq20
Distance traveled by a moving particle is equal to half of the product of instantaneous velocity and time. Which of the following statements is correct?
- a = constant
- v = constant
- a = zero
- v prop t2
Explanation
The distance traveled by the moving particle s, instantaneous velocity of the particle v and time t, according to the question,
An object is released from some height. Exactly after one second, another object is released from the same height. The distance between the two objects exactly after 2 seconds of the release of second object will be
- 4.9m
- 9.8m
- 19.6m
- 24.5m
Explanation
let, after two seconds the height of the first ball is h1 and height of the second ball is h1.
h1=1/2 × g × 3²
h2=1/2 × g × 2²
Then the distance between two balls will be
∴ h1- h2= 1/2 × g × 5 = 24.5 m
Two balls are dropped to the ground from different heights. One ball is dropped 2 sec after the other but they both strike the ground at the same time. If the first ball takes 3 sec to reach the ground then the difference in initial heights is:
- 7.8m
- 78m
- 15.6m
- 78.4m
Explanation
This question is similar to the question above, the second ball started journey two seconds after the first ball. And if the first ball travels five seconds, then the second ball travels three seconds.
Then the distance between two balls will be
A particle moves along a straight line OX. At a time t (in seconds ) the distance x (in meters) of the particle from O is given by
x(t) = 40 + 12t – t3
How long would the particle travel before coming to rest?
- 24m
- 40m
- 56m
- 16m
Explanation
Once you think of a moving object, when it will come to a rest! Yes, when the velocity of a moving object becomes zero, the moving object will come to rest. So, the equation of time with distance in question is given.
x = 40+12t -t³
When the object is at rest, the derivative will be zero in respect of time.
Therefore, distance will be
x = 40 + 24 -8 = 56m
A body moves along the curved path of a quarter circle. Calculate the ratio of distance to displacement
- 7 : 11
- 11 : 7
- 11 : 7√2
- 7 : 11√2
Explanation
You notice MCQ9, both questions are the same. And here we have to use its value instead of the pi symbol.
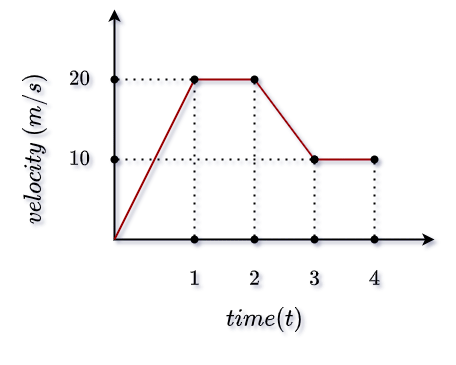
Variation of velocity of a particle moving along a straight line is shown in the figure. The distance traversed by the body in 4 seconds is
- 70m
- 60m
- 40m
- 55m
Explanation
The area of the velocity-time graph represents the distance.0-1s: (1/2 × 1 × 20) = 10
1-2s: (1 × 20) = 20
2-3s: (1/2 × 1 × 10) + (1 × 10) = 15
3-4s: (1 × 10) = 10Total distance cover in 0-4 seconds is 55 m.
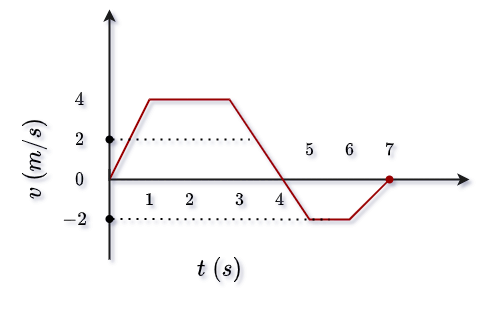
Velocity-time graph of a linear motion is shown below. The displacement from the origin after 8 seconds is
- 18m
- 16m
- 6m
- 4m
Explanation
The answer to this question is left for you, write the answer in the comment box below and send it.
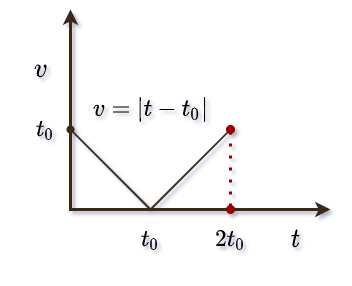
If a particle is moving at a speed of v=|t-t0| for 2t0 seconds, what is the distance traveled by the particle?
- 2t²0
- 3t²0
- t²0
- None
Explanation
If you draw a graph between velocity and time according to the given equation
The area of v-t according to the graph in first 2t0 seconds will be
d = 1/2 × t0 × t0 + 1/2 × t0 × t0 = t²0
A bird is flying in the sky along a straight line at v=|t-3| m/s speed. After 6 seconds the distance covered by the bird will be
- 6m
- 8m
- 9m
- 12m
Explanation
The answer to this question is left for you, write the answer in the comment box below and send it. Of course, its concept is similar to the mcq30 above.
If there is any mistake between the above question and answer, please let us know in the comment box below. The mistake will be corrected.
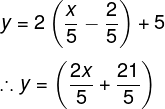
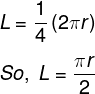
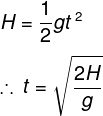
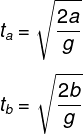
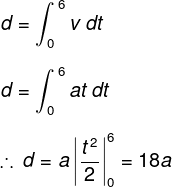
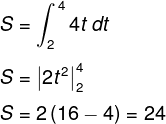
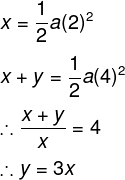
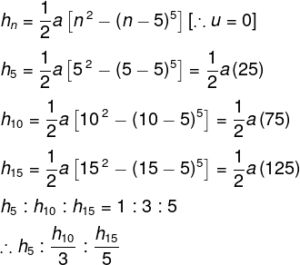
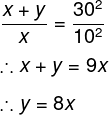
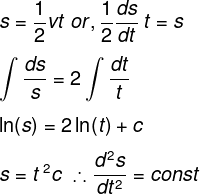
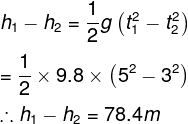
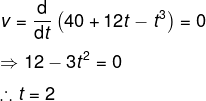
This website was… how do you say it? Relevant!! Finally I’ve found something that helped me. Many thanks!