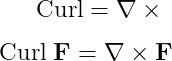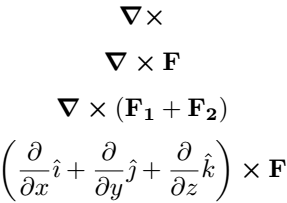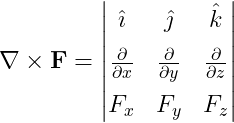The Curl operator is like a divergence operator. However, in the case of curl, there will be a cross-product between gradient and vector instead of the dot product.
\documentclass{article}
\begin{document}
\[ \textup{Curl}=\nabla\times \]
\[ \textup{Curl}\;\textbf{F}=\nabla\times\textbf{F} \]
\end{document}Output :
In latex, the best practice is to use the physics package for curl symbol as well, because the physics package contains a pre-defined \curl command that denotes the entire curl operator.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \curl \]
\[ \curl{\vb{F}} \]
\[ \curl(\vb{F_{1}}+\vb{F_{2}}) \]
\[ \qty(\pdv{x}\hat{\imath}+\pdv{y}\hat{\jmath}+\pdv{z}\hat{k})\cp \vb{F} \]
\end{document}Output :
The curl operation is also written in a matrix form. For this, you need to take the help of a matrix environment. And for matrix, you can use both amsmath or physics packages.
\documentclass{article}
\usepackage{amsmath,physics}
\begin{document}
\[ \nabla \cp \vb{F}= \begin{vmatrix}
\vu{\imath} & \vu{\jmath} & \hat{k}\\
\pdv{x} & \pdv{y} & \pdv{z}\\
F_{x} & F_{y} & F_{z}
\end{vmatrix} \]
\end{document}Output :