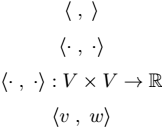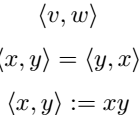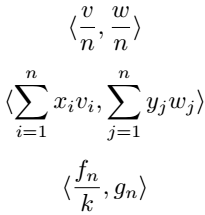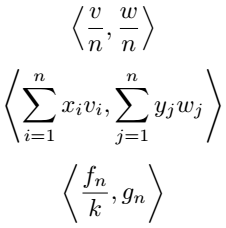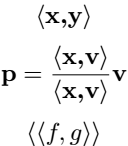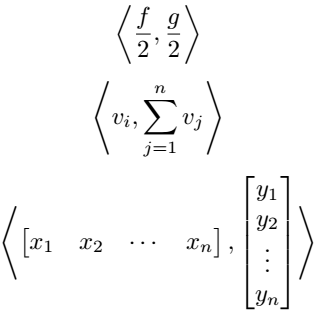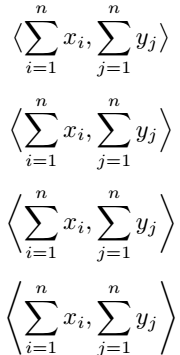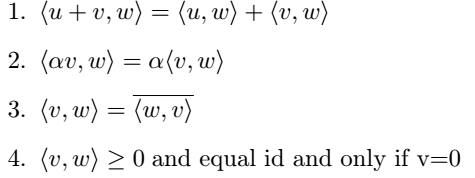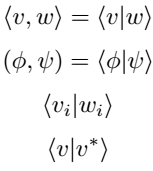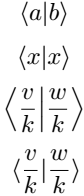How do you write an inner product〈a|b〉 in LaTeX?

The Inner product consists of a combination of two angle brackets in terms of shape, in which the elements are separated by a comma.

For full angle brackets, you need to use two separate \langel and \rangle commands.

\documentclass{article} 
\usepackage{amssymb}
\begin{document} 
  $$ \langle  \; , \; \rangle $$
  $$ \langle \cdot \; , \; \cdot \rangle $$
  $$ \langle \cdot \; , \; \cdot \rangle : V \times V  \rightarrow \mathbb{R} $$
  $$ \langle v \; , \; w \rangle $$
\end{document}

Output :

It is best practice to define a new command instead of \langle x, y \rangle syntax to use the inner product more than once in a document.

\documentclass{article}
\newcommand{\innerproduct}[2]{\langle #1, #2 \rangle}
\begin{document}
  $$ \innerproduct{v}{w} $$
  $$ \innerproduct{x}{y}=\innerproduct{y}{x} $$
  $$ \innerproduct{x}{y}:=xy $$
\end{document}

Output :

The main advantage of using a macro is that you can convert a latex syntax consisting of multiple commands into one short command.

But, you cannot mistakenly use keyboard less than and greater than symbols as angle brackets instead of latex commands. Because, there is a difference in shape between angel bracket and inequality symbol.

Responsive size of inner product

When the fraction part will be used as an element of the inner product. In that case, the angle bracket size and size of the element do not match properly.

\documentclass{article}
\newcommand{\innerproduct}[2]{\langle #1, #2 \rangle}
\begin{document}
  $$ \innerproduct{\frac{v}{n}}{\frac{w}{n}} $$
  $$ \innerproduct{\sum_{i=1}^{n}x_iv_i}{\sum_{j=1}^{n}y_jw_j} $$
  $$ \innerproduct{\frac{f_n}{k}}{g_n} $$
\end{document}

Output :

To solve this problem you need to use \left before \langel and \right before \rangel.

\documentclass{article}
\newcommand{\innerproduct}[2]{\left\langle #1, #2 \right\rangle}
\begin{document}
  $$ \innerproduct{\frac{v}{n}}{\frac{w}{n}} $$
  $$ \innerproduct{\sum_{i=1}^{n}x_iv_i}{\sum_{j=1}^{n}y_jw_j} $$
  $$ \innerproduct{\frac{f_n}{k}}{g_n} $$
\end{document}

Output :

Use mathtools package for inner product symbol

You can use the mathtools package to get the same output. And the most important command in this package is DeclarePairedDelimiter.

First, you can accomplish the same task using the DeclarePairedDelimiter command instead of the newcommand. For example

\documentclass{article}
\usepackage{mathtools}
\DeclarePairedDelimiter\innerproduct{\langle}{\rangle}
\begin{document}
  $$ \innerproduct{\textbf{x,y}} $$
  $$ \textbf{p}=\frac{\innerproduct{\textbf{x,v}}}{\innerproduct{\textbf{x,v}}}\textbf{v} $$
  $$ \innerproduct{\innerproduct{f,g}} $$
\end{document}

Output :

Second, the main advantage of using the mathtools package is that there is no need to use left and right commands separately for angle brackets of responsive size. Simply entering the * symbol with the define command is sufficient.

\documentclass{article}
\usepackage{mathtools}
\DeclarePairedDelimiter\innerproduct{\langle}{\rangle}
\begin{document}
  $$ \innerproduct*{\frac{f}{2},\frac{g}{2}} $$
  $$ \innerproduct*{v_i,\sum_{j=1}^{n}v_j} $$
  $$ \innerproduct*{\begin{bmatrix} x_{1} & x_{2} & \cdots & x_{n}\end{bmatrix}, \begin{bmatrix} y_{1} \\ y_{2} \\ \vdots \\ y_{n} \end{bmatrix}}$$
\end{document}

Output :

Third, you can pass four types of big commands as optional arguments with new defined command.

\documentclass{article}
\usepackage{mathtools}
\DeclarePairedDelimiter\innerproduct{\langle}{\rangle}
\begin{document}
  $$ \innerproduct[\big]{\sum_{i=1}^{n}x_i,\sum_{j=1}^{n}y_j} $$
  $$ \innerproduct[\Big]{\sum_{i=1}^{n}x_i,\sum_{j=1}^{n}y_j} $$
  $$ \innerproduct[\bigg]{\sum_{i=1}^{n}x_i,\sum_{j=1}^{n}y_j} $$
  $$ \innerproduct[\Bigg]{\sum_{i=1}^{n}x_i,\sum_{j=1}^{n}y_j} $$
\end{document}

Output :

All properties of inner product in LaTeX

The inner product has four to five properties which are represented below with the help of latex.

\documentclass{article}
\newcommand{\ip}[2]{\langle #1, #2 \rangle}
\begin{document}
 \begin{enumerate}
  \item  $ \ip{u+v}{w}=\ip{u}{w}+\ip{v}{w} $
  \item  $ \ip{\alpha v}{w} =\alpha \ip{v}{w} $
  \item  $ \ip{v}{w}=\overline{\ip{w}{v}} $
  \item  $ \ip{v}{w}\geq 0\;\textrm{and equal id and only if v=0} $
 \end{enumerate}
\end{document}

Output :

Use bra-ket notation for inner product

In many cases, the inner product is represented by bra-ket notation. In the case of bracket notation, a single bar is used instead of a comma with an angle bra-ket. For example

\documentclass{article}
\newcommand{\innerp}[2]{\left\langle #1 \vert #2 \right\rangle}
\begin{document}
  $$ \langle v,w \rangle = \innerp{v}{w} $$
  $$ ( \phi,\psi ) = \innerp{\phi}{\psi} $$
  $$ \innerp{v_i}{w_i} $$ 
  $$ \innerp{v}{v^*} $$ 
\end{document}

Output :

Bra-ket notation plays an important role in physics. For this reason, you can use the physics package to denote bra-ket notation. Which contains pre-defined braket command.

\documentclass{article}
\usepackage{physics}
\begin{document}
  $$ \braket{a}{b} $$
  $$ \braket{x} $$
  $$ \braket{\frac{v}{k}}{\frac{w}{k}} $$
  $$ \braket*{\frac{v}{k}}{\frac{w}{k}} $$
\end{document}

Output :