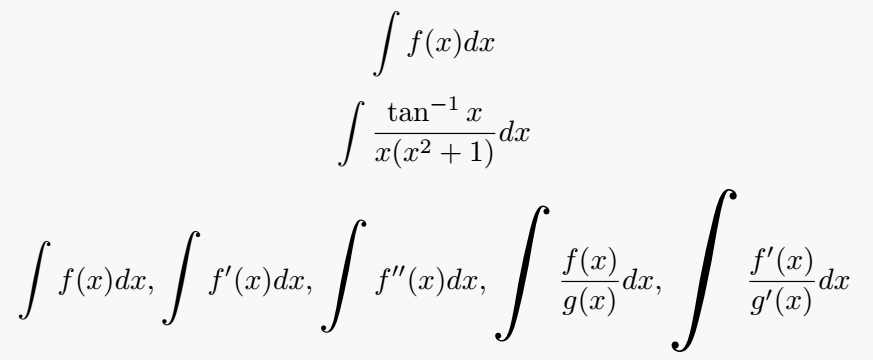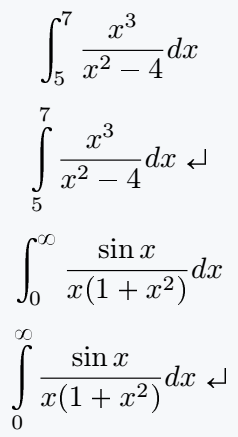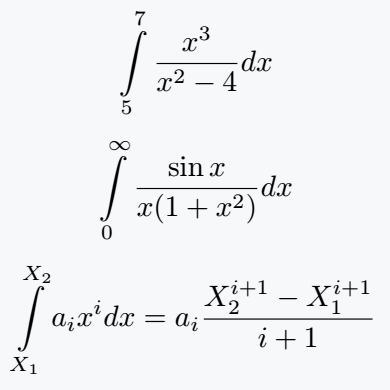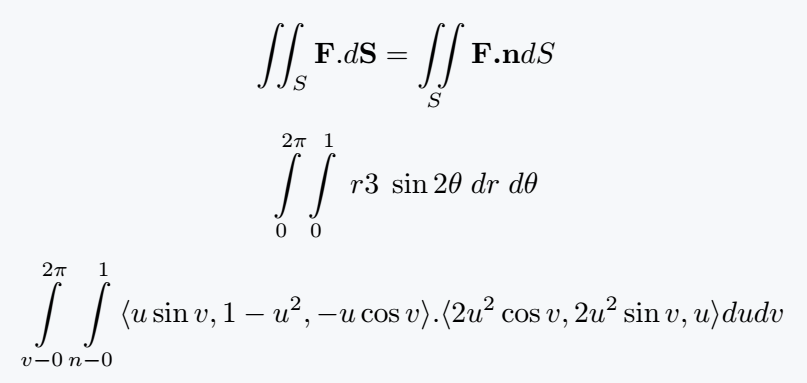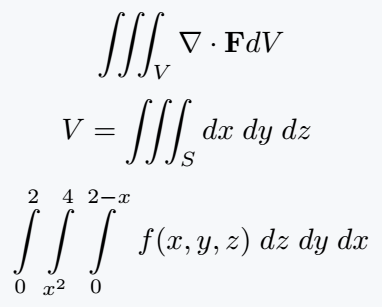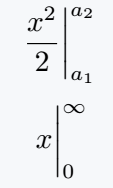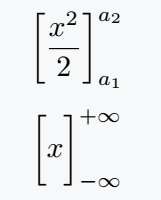The default command to show the integral symbol in a document is \int. It’s the one most people use.
If you want to make the integral symbol bigger, you can use the bigints package, which lets you enlarge it step by step.
\documentclass{article}
\usepackage{bigints}
\begin{document}
\[ \int f(x) dx \]
\[ \int \frac{\tan^{-1}x}{x(x^2+1)}dx \]
\[ \bigintssss f(x)dx ,\bigintsss f'(x)dx ,\bigintss f''(x)dx,\bigints \frac{f(x)}{g(x)}dx,\bigint \frac{f'(x)}{g'(x)}dx \]
\end{document}Output :
Integral symbol with above and below limits
The other way is to place the limits above and below the integral symbol. For that, you’ll need to use the \limits command with \int.
\documentclass{article}
\begin{document}
\[ \int_5^7 \frac{x^3}{x^2-4}dx \]
\[ \int\limits_5^7 \frac{x^3}{x^2-4}dx \]
\[ \int_0^\infty \frac{\sin x}{x(1+x^2)}dx \]
\[ \int\limits_0^\infty \frac{\sin x}{x(1+x^2)}dx \]
\end{document}Output :
As you can see from the examples, the output looks a little different depending on the method you choose.
Rather than writing all those commands every time, you can simplify things by creating one command using \newcommand. This way, it’s faster and cleaner.
\documentclass{article}
\usepackage{bigints}
\newcommand{\integral}[2]{\int\limits_{#1}^{#2}}
\begin{document}
\[ \integral{5}{7} \frac{x^3}{x^2-4}dx \]
\[ \integral{0}{\infty}\frac{\sin x}{x(1+x^2)}dx \]
\[ \integral{X_1}{X_2}a_i x^i dx= a_i \frac{X^{i+1}_2 - X^{i+1}_1}{i+1}\]
\end{document}Output :
Double integral symbol(Surface integral)
For double integrals, you’ll have to use limits twice with the \int command-once for each integral.
\documentclass{article}
\usepackage{amsmath}
\newcommand{\integral}[2]{\int\limits^{#1}_{#2}}
\begin{document}
\[ \iint_S \textbf{F}.d\textbf{S}= \iint\limits_S \textbf{F.n}dS \]
\[ \integral{2\pi}{0}\integral{1}{0} \;r3\; \sin 2\theta\; dr \;d\theta \]
\[ \integral{2\pi}{v-0}\integral{1}{n-0}\langle u\sin v,1-u^2,-u\cos v\rangle.\langle 2u^2\cos v,2u^2 \sin v,u\rangle dudv \]
\end{document}Output :
If you only need to use limits below the symbol, just using \iint for the double integral will do the job.
Triple integral symbol
For triple integrals, you’ll write it in a similar way, but here, you’ll need to use the \iiint command. It works specifically for triple integrals.
\documentclass{article}
\usepackage{amsmath}
\newcommand{\integral}[2]{\int\limits^{#1}_{#2}}
\begin{document}
\[ \iiint_V \nabla \cdot\textbf{F}dV \]
\[ V =\iiint_S dx\; dy\; dz\; \]
\[ \integral{2}{0}\integral{4}{x^2}\integral{2-x}{0}\; f(x,y,z)\;dz\;dy\;dx \]
\end{document}Output :
Closed integral symbol
If you want to use closed integrals, the Pxfonts package has you covered with all the necessary commands. You can also find similar symbols in other packages like stix or mathabx.
\documentclass{article}
\usepackage{pxfonts}
\begin{document}
\[ \oint,\ointclockwise,\ointctrclockwise \]
\[ \oiint,\oiintclockwise,\oiintctrclockwise \]
\[ \oiiint,\oiiintclockwise,\oiiintctrclockwise \]
\[ \sqint,\sqiint,\sqiiint \]
\end{document}Output :
Integral evaluation bar
You can manually create an integration evaluation bar if you need it. Or, you can use the \eval command from the physics package, which solves this easily in a couple of ways.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[\frac{x^2}{2} \bigg|_{a_1}^{a_2} \]
\[ \eval{x}_0^\infty \]
\end{document}Output :
Square brackets with a limit
For square brackets, you’ll want to make sure they’re bigger than the expression inside. To do this, you can use the \bigg command.
This way, you can add superscripts and subscripts to apply limits properly.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \bigg[\frac{x^2}{2} \bigg]_{a_1}^{a_2} \]
\[ \bqty\bigg{x}_{-\infty}^{+\infty} \]
\end{document}Output :