LaTeX provides two main ways of representing mathematical expressions within a text and mathematical equations that appear on separately on an independent line or paragraph.
In this article, we are going to see how to present our mathematical expression in the two forms presented above.
Inline Math Mode
When mathematical expressions or symbols appear within a text, we refer to those expressions as being in inline mode when we are typesetting them.
LATEX provides us with 3 ways to typeset mathematical expressions in the inline math mode and they include:
1. $ . . .$
2. \begin{math} . . . \end{math}
3. \( . . . \)
Below is an example demonstrating the use of the 3 different methods to implement mathematical expressions with a blog of text in math mode. Begin by loading \usepackage{amsmath} in your preamble i.e
\documentclass{article}
\usepackage{amsmath}
\begin{document}
.
.
.
\end{document}Let start with
Case 1. $….$
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Suppose that $g(x) \leq f(x) \leq h(x)$ for all $x$ in some open interval containing $c$,
except possibly at $x = c$ itself. Suppose also that $ \lim_{x \to c}g(x) = \lim_{x \to c}h(x) = L$.
Then $\lim_{x \to c}f(x) = L$. This is called the Sandwish Theorem.
\end{document}Output :
Case 2. \begin{math} . . . \end{math}
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Suppose that \begin{math}g(x) \leq f(x) \leq h(x)\end{math} for all
\begin{math}x\end{math} in some open interval containing \begin{math}c\end{math},
except possibly at \begin{math}x =c\end{math} itself.
Suppose also that \begin{math}\lim_{x \to c}g(x) =\lim_{x \to c}h(x) = L\end{math}.
Then\begin{math}\lim_{x \to c}f(x) = L\end{math}. This is called the Sandwish Theorem.
\end{document}Output :
Case 3. \( . . . \)
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Suppose that \(g(x) \leq f(x) \leq h(x)\) for all \(x\) in
some open interval containing \(c\), except possibly at \(x = c\)
itself. Suppose also that \(\lim_{x \to c}g(x) = \lim_{x \to c}h(x) = L\).
Then \(\lim_{x \to c}f(x) = L\). This is called the Sandwish Theorem.
\end{document}Output :
Above 3 cases demonstrate clearly how to typeset a blog of text that contains mathematical expressions hence a blog of text in the inline math mode.
Display Math Mode
When the mathematical expressions or equations appear independently on a separate line with or without an equation number, these expressions are referred to be in the display mode when typesetting them.
LaTeX provides us with 3 ways to typeset mathematical expressions or equations in an independent line or new paragraph that is, in the display math mode and they include:
1. $$ . . .$$
2. \begin{displaymath} . . . \end{displaymath}
3. \[ . . . \]
Now, lets look at how to implement the display math mode.
Case 1: $$ . . .$$
$$...$$ is used to typeset display-style mathematical equations. It creates a standalone block of math content that is centered on a new line, separate from the surrounding text.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
A set of $ mn $ number (real or imaginary) arranged in the
form of a rectangular array of $ m $ rows and $ n $ columns
is called an $ m \times n $ matrix. An $ m \times n $ matrix
is usually written as
$$
A =\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}
$$
\end{document}Output :
Case 2: \begin{displaymath} . . . \end{displaymath}
\documentclass{article}
\usepackage{amsmath}
\begin{document}
A set of $ mn $ number (real or imaginary) arranged in the
form of a rectangular array of $ m $ rows and $ n $ columns
is called an $ m \times n $ matrix. An $ m \times n $ matrix
is usually written as
\begin{displaymath}
A =\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}
\begin{displaymath}
\end{document}Output :
Case 3: \[ . . .\]
\documentclass{article}
\usepackage{amsmath}
\begin{document}
A set of $ mn $ number (real or imaginary) arranged in the
form of a rectangular array of $ m $ rows and $ n $ columns
is called an $ m \times n $ matrix. An $ m \times n $ matrix
is usually written as
\begin{displaymath}
A =\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n}\\
a_{21} & a_{22} & \cdots & a_{2n}\\
\vdots & \vdots & \ddots & \vdots\\
a_{n1} & a_{n2} & \cdots & a_{nn}
\end{pmatrix}
\begin{displaymath}
\end{document}Output :
The 3 cases above demonstrate clearly how to typeset mathematical expression in display math mode (In a new paragraph or a separate independent line).
Conclusion
This article gives you a full coverage of how to present mathematical expressions both in in-line math mode and display math mode.
This is the most important and fundamental concept to know when working with LaTeX.
Out of the 3 cases we have seen in both in-line and display math mode.
It is often advisable and agree upon by many LaTeX typesetters to use $....$ for in-line mathematics and \[ . . .\] for display mathematics and the most prominent reason for this chose is readability.

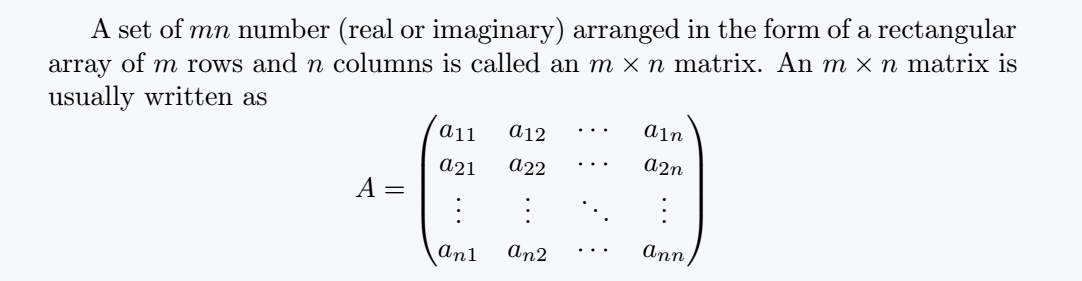
Medicine