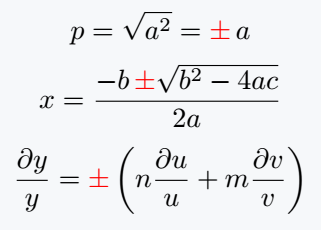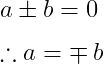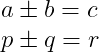In this guide, we will explain how to create the plus-minus symbol (±) in LaTeX by using the \pm command. It is very simple because you do not need to pass any argument.
Using \pm Command
To make the plus-minus symbol, simply use the \pm command. This symbol is often used in math, for example when finding the square root of a number.
\documentclass{article}
\usepackage{xcolor}
\begin{document}
\[ p=\sqrt{a^{2}}={\color{red}\pm}\,a \]
\[ x= \frac{-b\,{\color{red}\pm}\sqrt{b^2 -4ac}}{2a} \]
\[ \frac{\partial y}{y}= {\color{red}\pm}\left( n\frac{\partial u}{u} + m\frac{\partial v}{v} \right) \]
\end{document}
In this example, the \sqrt{arg} command is used to show the square root. The \pm command is used to display the ± symbol.
Text Mode
You cannot use \pm directly in text mode. To fix this, include the textcomp package. Then you can use the \textpm command to show the symbol in normal text.
\(\textpm\)
Minus-Plus Symbol
If you need the minus-plus symbol (∓), which is the reverse of the plus-minus symbol, use the \mp command. For example,
\documentclass{article}
\begin{document}
\[ a\pm b=0 \]
\[ \therefore a=\mp b \]
\end{document}Output :
Using Multiple Packages
You can also use the \pm command with different LaTeX packages. Here is an example using the packages MnSymbol, fdsymbol, boisik, and stix.
\documentclass{article}
\usepackage{MnSymbol}
\begin{document}
\[ a \pm b = c \]
\[ p \pm q = r \]
\end{document}Output :
Conclusion
In this guide, we learned how to use the \pm and \mp commands in LaTeX. We saw how to use these commands in math mode and in text mode. We also looked at different packages that support these commands.
