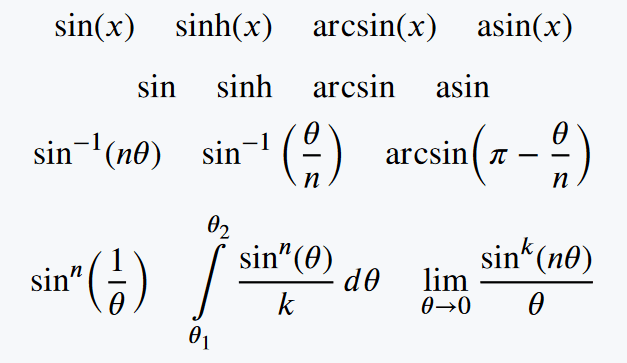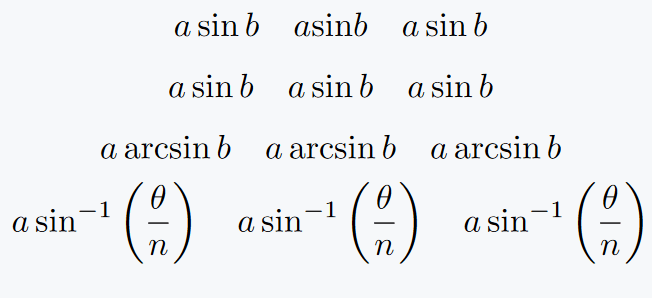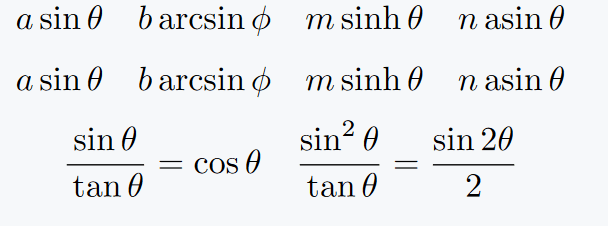All trigonometric functions related to sin are represented in this tutorial. A simple command to represent sin is \sin . You can convert to inverse sin using superscript with this command like \sin^{-1}.
\documentclass{article}
\begin{document}
\[\sin\theta ,\, \sin^{-1}(\theta),\, \arcsin(\theta), \; \sinh\left(\frac{n\theta}{k}\right)\]
\[\sin{\frac{\theta}{n}},\,\sin^{-1}\left(\pi-\frac{\theta}{n}\right)\]
\[\int\limits_{\pi}^{\frac{\pi}{2}}\frac{\sin\theta}{\theta}\mathrm{d\theta},\,\int\limits_{\pi}^{\left(\pi-\frac{1}{2}\right)}\hspace{-10px}\sin^{-1}\left(\frac{\sin\theta}{\theta}\right)\mathrm{d\theta}\]
\[\lim_{\theta \to 0}\frac{\sin\theta}{\theta} , \,\lim_{\theta \to 0} \frac{\sin(\pi-n\theta)}{\theta}\]
\end{document}Output :
Not all functions are stocked by default in this tutorial.
Use physics package
Second option, we have is physics package which contains all trigonometric functions. and can add direct powers or superscripts to commands using optional arguments.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \sin(x) \quad \sinh(x) \quad \arcsin(x) \quad \asin(x) \]
\[ \sine \quad \hypsine \quad \arcsine \quad \asine \]
\[\sin[-1](n\theta) \quad \sine^{-1}\left(\frac{\theta}{n}\right) \quad \arcsin(\pi - \frac{\theta}{n})\]
\[ \sin[n](\frac{1}{\theta}) \quad \int\limits_{\theta_1}^{\theta_2}\frac{\sin[n](\theta)}{k}\,d\theta \quad \lim_{\theta \to 0}\frac{\sin[k](n\theta)}{\theta} \]
\end{document}Output :
Third is my best method which has no limitations. This method will not return a direct function command but rather an mathematics function font.
Use mathrm and operatorname command
mathrm{arg} and operatorname{arg}, in which the function name must be passed as an argument. Even if operatorname{arg} handles space. But, mathrm{arg} needs to add a little space on both sides.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ a \sin b \quad a \mathrm{sin} b \quad a \operatorname{sin} b \]
\[ a \sin b \quad a \, \mathrm{sin} \, b \quad a \operatorname{sin} b \]
\[ a \arcsin b \quad a \, \mathrm{arcsin} \, b \quad a \operatorname{arcsin} b \]
\[ a \sin^{-1}\left(\frac{\theta}{n}\right) \quad a \, \mathrm{sin}^{-1}\left(\frac{\theta}{n}\right) \quad a \operatorname{sin}^{-1}\left(\frac{\theta}{n}\right)\]
\end{document}Output :
Suppose you are creating a document that contains many mathematical functions. In that case, you can define a new math function using this opratorname{arg} or mathrm{arg} with the newcommand.
\documentclass{article}
\usepackage{amsmath}
\newcommand{\func}[1]{\operatorname{#1}}
\newcommand{\funct}[1]{\,\mathrm{#1}\,}
\begin{document}
\[ a\func{sin}\theta \quad b\func{arcsin}\phi \quad m\func{sinh}\theta \quad n \func{asin}\theta \]
\[ a\funct{sin}\theta \quad b\funct{arcsin}\phi \quad m\funct{sinh}\theta \quad n \funct{asin}\theta \]
\[\frac{\func{sin}\theta}{\funct{tan}\theta} = \cos\theta \quad \frac{\func{sin}^2\theta}{\funct{tan}\theta} = \frac{\sin2\theta}{2}\]
\end{document}Output :
You don’t need to use separate commands. Just pass the function name into the new define command and the job is done.
