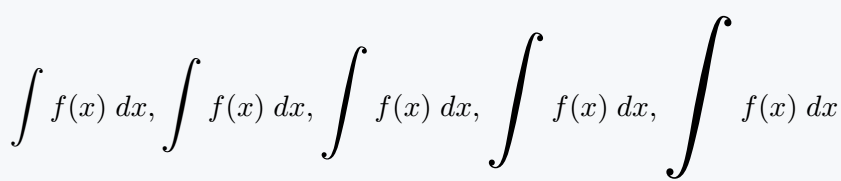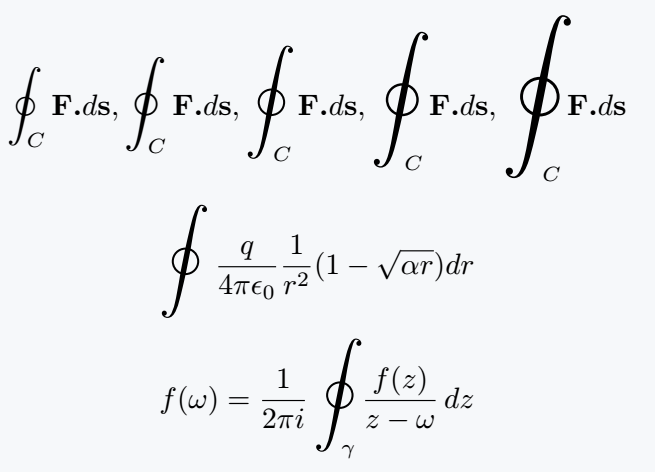To make a document beautiful, every symbol and expression of latex must match. For this reason, Big Symbol will be needed from time to time.
The popular package for big integral symbol is bigints, in which different commands are defined in sequence.
\documentclass{article}
\usepackage{bigints}
\begin{document}
\[ \bigintssss f(x)\;dx,\bigintsss f(x)\;dx,\bigintss f(x)\;dx,\bigints f(x)\;dx,\bigint f(x)\;dx \]
\end{document}Output :
Big integral symbol with limits
Since the size of the integral symbol is large. So, there is no need to use the \limits command. So the limit has been used with the direct big integral symbol
\documentclass{article}
\usepackage{xfrac,bigints}
\begin{document}
\[ \bigintss_0^1\frac{\tan^{-1}(\sqrt{x^2+1})}{(x^2+1)^{\sfrac{3}{2}}} \]
\[ \bigints_0^\pi\left(\frac{1}{1-\frac{2\alpha}{1+\alpha^2}\cos x}\right)dx \]
\[ \bigint_0^1 \sqrt{\frac{\int_a^b(fx,y,z)dx+\frac{\int_a^b \alpha(x,y,z)dx}{\beta}}{\int_a^b g(x,y,z)dx}}\;dydz \]
\end{document}Output :
Close integral symbol in LaTeX
In the same way, the command is defined in chronological order for Big Close integral. Which is shown in the following code.
\documentclass{article}
\usepackage{bigints}
\begin{document}
\[ \bigointssss_C\textbf{F.}d\textbf{s},\bigointsss_C\textbf{F.}d\textbf{s},\bigointss_C\textbf{F.}d\textbf{s},\bigoints_C\textbf{F.}d\textbf{s},\bigoint_C\textbf{F.}d\textbf{s} \]
\[\bigointss\frac{q}{4\pi\epsilon_0}\frac{1}{r^2}(1-\sqrt{\alpha r})dr \]
\[ f(\omega)=\frac{1}{2\pi i}\bigointss_\gamma\frac{f(z)}{z-\omega}\,dz \]
\end{document}Output :