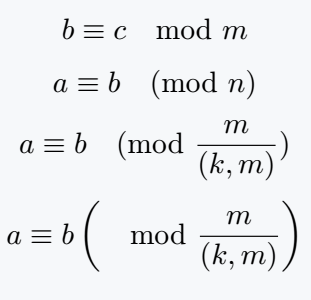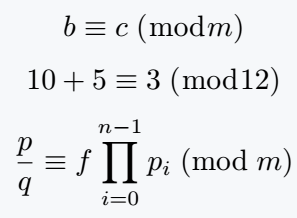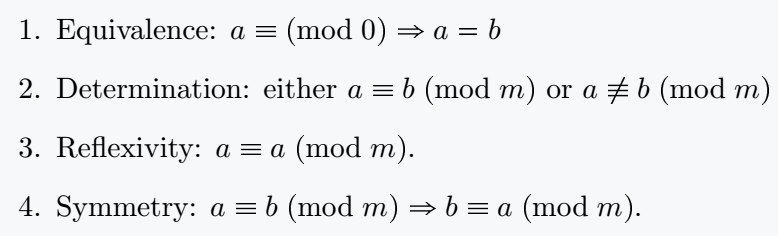Congruence modulo syntax will consist of two individual commands, \equiv and \mod commands.
\documentclass{article}
\usepackage{mathtool}
\begin{document}
% Use mathtools for \mod
\[ b \equiv c \mod{m} \]
% \pmod is default command
\[ a \equiv b \pmod{n} \]
\[ a \equiv b \pmod{\frac{m}{(k,m)}} \]
\[ a \equiv b \left(\mod{\frac{m}{(k,m)}}\right) \]
\end{document}Output :
But, you notice the output above, where a lot of space has been created by using the \mod and \pmod commands.
To solve this problem you need to use \bmod command, or manually solve using \mathrm command.
\documentclass{article}
\begin{document}
\[ b \equiv c\;(\bmod{m}) \]
\[ 10+5 \equiv 3\;(\bmod{12}) \]
\[ \frac{p}{q} \equiv f\prod^{n-1}_{i=0}p_i\;(\mathrm{mod}\;m) \]
\end{document}Output :
Some congruence modulo proparties in LaTeX
Best practice is shown by discussing some properties below.
\documentclass{article}
\usepackage{mathabx}
\begin{document}
\begin{enumerate}
\item Equivalence: $ a \equiv \modx{0}\Rightarrow a=b $
\item Determination: either $ a\equiv b\; \modx{m} $ or $ a \notequiv b\; \modx{m} $
\item Reflexivity: $ a\equiv a \;\modx{m} $.
\item Symmetry: $ a\equiv b\; \modx{m}\Rightarrow b\equiv a \;\modx{m} $.
\end{enumerate}
\end{document}Output :