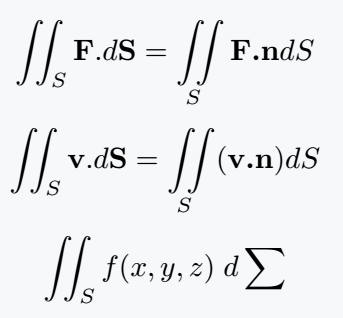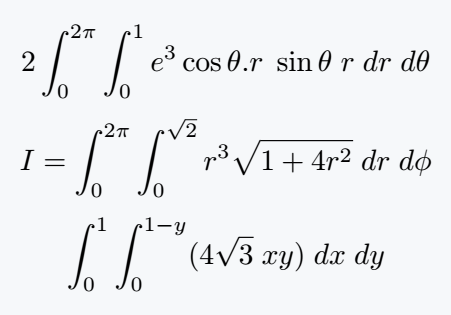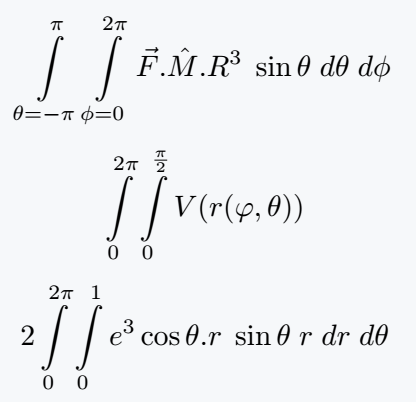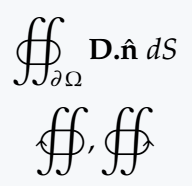How to write a double integral(∬, ∯) in LaTeX?

Double integral or surface integral is formed by the combination of two integrals.

Even if double limit is used without limit, in the case of surface integral, lower limit S and A have to be used.

Only S has been passed within the lower limit below.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
   $$ \iint_S \textbf{F}.d\textbf{S}= \iint\limits_S \textbf{F.n}dS $$
   $$ \iint_S \textbf{v}.d\textbf{S}= \iint\limits_S (\textbf{v.n})dS $$
   $$ \iint_S f(x,y,z)\;d\sum $$ 
\end{document}

Output :

Double integral[surface integral] symbol with limits in LaTeX

For limit, you have to use subscript and superscript with Integral symbol. You can use \newcommnad instead of typing the same expression over and over again.

\documentclass{article}
\begin{document}
   $$ 2\int_0^{2\pi}\int_0^1 e^3 \cos\theta.r\;\sin\theta\; r\;dr\;d\theta $$
   $$ I=\int_0^{2\pi}\int_0^{\sqrt{2}}r^3\sqrt{1+4r^2}\;dr\;d\phi $$
   $$ \int_0^1\int_0^{1-y}(4\sqrt{3}\;xy)\;dx\;dy $$
\end{document}

Output :

To use the limit above and below the integral symbol, you need to use the \limits command separately.

\documentclass{article}
\usepackage{amsmath}
\newcommand{\integral}[4]{\int\limits^{#1}_{#2}\int\limits^{#3}_{#4}}
\begin{document}
   $$ \integral{\pi}{\theta=-\pi}{2\pi}{\phi=0}\vec{F}.\hat{M}.R^3\;\sin\theta\;d\theta\;d\phi $$
   $$ \integral{2\pi}{0}{\frac{\pi}{2}}{0} V(r(\varphi,\theta)) $$
   $$ 2\integral{2\pi}{0}{1}{0} e^3 \cos\theta.r\;\sin\theta\; r\;dr\;d\theta $$
\end{document}

Output :

Of course, you can see by looking at the above two outputs, in which case using the \limits command would be the best practice!

Surface closed integral symbol in LaTeX

In case of double closed integral, there is no limit. However, S or A is used as a lower limit in the case of surface integral.

\documentclass{article}
\usepackage{pxfonts}
\begin{document}
   $$ \oiint_{\partial\,\Omega}\textbf{D.}\hat{\textbf{n}}\;dS $$
   $$ \oiintclockwise,\oiintctrclockwise $$
\end{document}

Output :