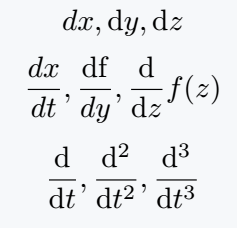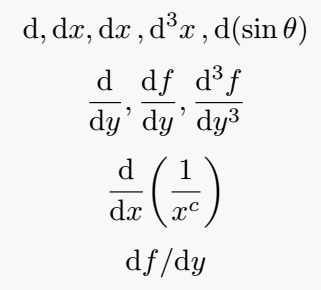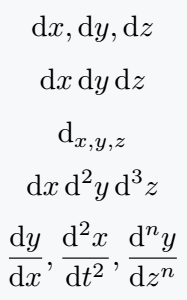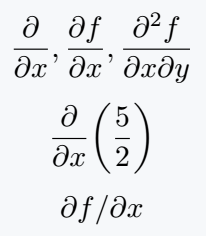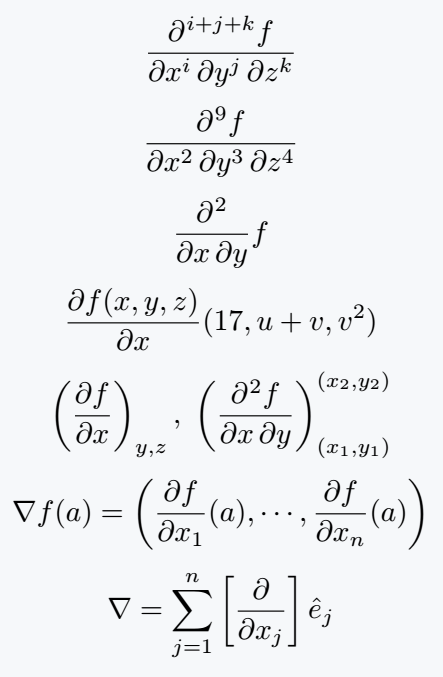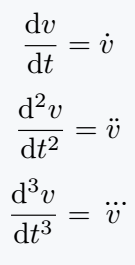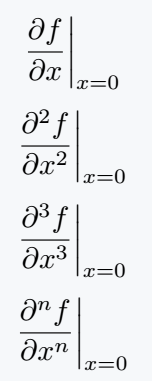How do you write derivatives in LaTeX?

First of all, you will try to represent the derivative in the document by passing multiple expressions in the fraction.

\mathrm{arg}
\frac{arg1}{arg2}

\documentclass{article}
\begin{document}
  \[ {dx},\mathrm{d}y, \mathrm{d}z \]
  \[ \frac{dx}{dt}, \frac{\mathrm{df}}{dy}, \frac{\mathrm{d}}{\mathrm{d}z}f(z) \]
  \[ \frac{\mathrm{d}}{\mathrm{d}t}, \frac{\mathrm{d^2}}{\mathrm{d}t^2}, \frac{\mathrm{d^3}}{\mathrm{d}t^3} \]
\end{document}

Output :

But, why would you use such a big syntax again and again! And for some more limitations, derivatives and physics packages have been created in Latex.

Use physics and derivative for LaTeX

\dv command is included in the physics package for ordinary derivatives. And in this case, syntax are

\dv{arg}
\dd[order]{arg}
\dv{arg1}{arg2}
\dv*{arg1}{arg2}
\dv[order]{arg1}{arg2}

\documentclass{article}
\usepackage{physics}
\begin{document}
  % Use physics package for Differentials
  \[ \dd, \dd x, \dd{x}, \dd[3]{x}, \dd(\sin\theta) \]
  \[ \dv{y}, \dv{f}{y}, \dv[3]{f}{y} \]
  \[ \dv{x}(\frac{1}{x^c}) \]    
  % Inline form for text mode
  \[ \dv*{f}{y} \]
\end{document}

Output :

However, in a derivative package, both command and syntax are different from physics. Order value must be given as an optional argument for the order.

\odif{arg1,arg2,arg3}
\odif*{arg1,arg2,arg3}
\odif[order={order1,order2,order3,..}]{arg1,arg2,arg3,..}
\odv[order={value}]{arg1}{arg2}

\documentclass{article}
\usepackage{derivative}
\begin{document}
   % Use derivative package for Differentials
   \[ \odif{x}, \odif{y}, \odif{z} \]
   \[ \odif{x,y,z} \]
   \[ \odif*{x,y,z} \]
   \[ \odif[order={1,2,3}]{x,y,z} \] 
   \[ \odv{y}{x}, \odv[order={2}]{x}{t}, \odv[order={n}]{y}{z} $
\end{document}

Output :

Use partial derivatives

Manually, there are \partial commands for partial derivatives. But, I will use physics package where there is \pdv command.

\pdv{arg}
\pdv{arg1}{arg2}{arg3}
\pdv*{arg1}{arg2}

\documentclass{article}
\usepackage{physics}
\begin{document}
   \[ \pdv{x},\pdv{f}{x}, \pdv{f}{x}{y} \]
   \[ \pdv{x}(\frac{5}{2})   \]
   % inline form for partialderivative
   \[ \pdv*{f}{x}  \]
\end{document}

Output :

This package has the same command. However, there are many features that are not included in the physics package. For this reason, in the case of partial derivatives, the best practice is to use the derivative package.

\pdv[order={order1,order2,order3,..}]{arg1}{arg1,arg2,arg3,..}
\pdv{arg1}{arg2}_{arg3}^{arg4}
\sum
\nabla
\hat{arg}
\cdots

\documentclass{article}
\usepackage{derivative}
\begin{document}
   \[ \pdv[order={i,j,k}]{f}{x,y,z} \]
   \[ \pdv[order={2,3,4}]{f}{x,y,z} \]
   \[ \pdv*{f}{x,y} \]
   \[ \pdv{f(x,y,z)}{x}(17,u+v,v^2) \]
   \[ \pdv{f}{x}_{y,z},\; \pdv{f}{x,y}^{(x_2,y_2)}_{(x_1,y_1)} \]
   \[ \nabla f(a)=\left(\pdv{f}{x_1}(a),\cdots,\pdv{f}{x_n}(a) \right) \]
   \[ \nabla = \sum_{j=1}^n\left[\pdv{}{x_j} \right]\hat{e}_j \]
\end{document}

Output :

Dot derivative in LaTeX

There is no special package or command for dot or time derivative, manually represented below.

\dot{arg}
\ddot{arg}
\dddot{arg}

\documentclass{article}
\usepackage{physics}
\begin{document}
   % \dot and \ddot is a default command in latex   
   \[ \dv{v}{t} = \dot{v} \]
   \[ \dv[2]{v}{t} = \ddot{v} \]
   % \dddot is a physics package's command
   \[ \dv[3]{v}{t} = \dddot{v} \]
\end{document}

Output :

Use evaluated bar

Evaluated bar is used when the value of the variable is given along with the derivative. If you pass the expression in a short command \eval, the whole expression will be completed.

\eval{exp}_{arg1}^{arg2}

\documentclass{article}
\usepackage{physics}
\begin{document}
   \[ \eval{\pdv{f}{x}}_{x=0} \]
   \[ \eval{\pdv[2]{f}{x}}_{x=0} \]
   \[ \eval{\pdv[3]{f}{x}}_{x=0} \]
   \[ \eval{\pdv[n]{f}{x}}_{x=0} \]
\end{document}

Output :