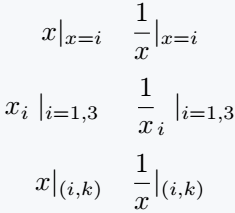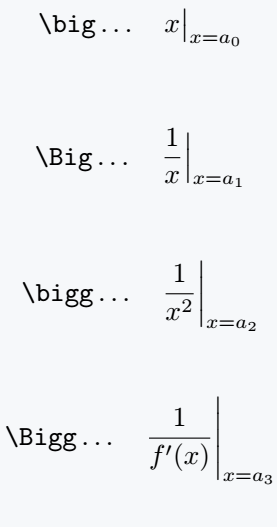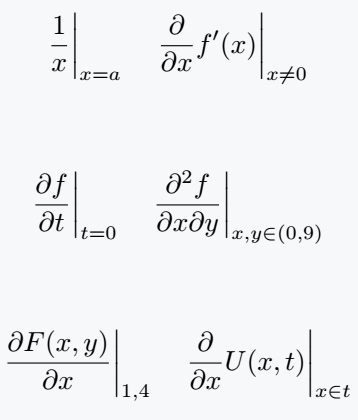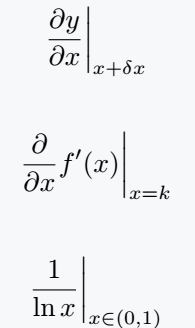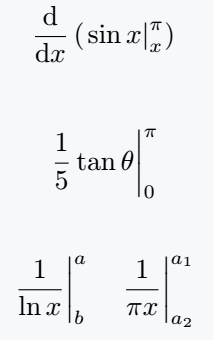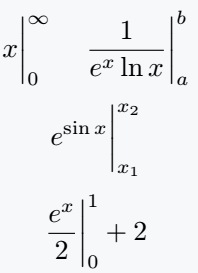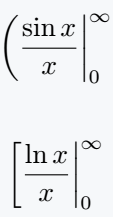Main problem with evaluate limit or bar is the size of the delimiters.
Because, if you use a direct vertical bar, it will be adjustable with vertically small size expression but in most cases, it will not be adjustable.
However, a single bar is used for the evaluation bar. Which is located on the right side of the expression. Multiple commands are used to identify the pipe.
But, the rvert command and vertical bar are best practice for positioning on the right side of the expression.
Of course, you have to call the amsmath package for this command. Otherwise, it will show an error.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ x|_{x=i} \quad \frac{1}{x}|_{x=i} \]
\[ x_i\mid_{i=1,3} \quad \frac{1}{x}_i\mid_{i=1,3} \]
\[ x\rvert _{(i,k)} \quad \frac{1}{x}\rvert _{(i,k)} \]
\end{document}Output :
With the help of LaTeX, you can manually increase the size of the vertical bar or adjust it automatically with the expression.
Manually adjustment
As you may know, four big(\big,\Big,\bigg,\Bigg) commands are used according to the sequence to increase the size of delimiters. I will use exactly the same method here.
\documentclass{article}
\begin{document}
\[ \verb|\big|\dots\quad x\big|_{x=a_0} \]
\[ \verb|\Big|\dots\quad \frac{1}{x}\Big|_{x=a_1} \]
\[ \verb|\bigg|\dots\quad \frac{1}{x^2}\bigg|_{x=a_2} \]
\[ \verb|\Bigg|\dots\quad \frac{1}{f'(x)}\Bigg|_{x=a_3} \]
\end{document}Output :
Automatic adjustable
Latex has a combination of \left and \right commands to automatically adjust the delimiters size. Cannot use both commands separately.
So, for the right vertical bar, you have to use the \left command along with the \right command.
\documentclass{article}
\begin{document}
\[ \left \frac{1}{x}\right|_{x=a} \quad \left \frac{\partial}{\partial x}f'(x)\right|_{x\neq0} \]
\[ \left \frac{\partial f}{\partial t}\right|_{t=0} \quad \left \frac{\partial^2f}{\partial x \partial y}\right|_{x,y\in(0,9)} \]
\[ \left \frac{\partial F(x,y)}{\partial x} \right|_{1,4} \quad \left \frac{\partial}{\partial x} U(x,t)\right|_{x\in t}\]
\end{document}Output :
Use single limit or double limits with the evaluate bar
Subscript is used for single limits. Which can be noticed in the case of derivatives.
If you want to replace the entire method with a new command, you can do it.
\documentclass{article}
\begin{document}
\[ \left \frac{1}{x}\right|_{x=a} \quad \left \frac{\partial}{\partial x}f'(x)\right|_{x\neq0} \]
\[ \left \frac{\partial f}{\partial t}\right|_{t=0} \quad \left \frac{\partial^2f}{\partial x \partial y}\right|_{x,y\in(0,9)} \]
\[ \left \frac{\partial F(x,y)}{\partial x} \right|_{1,4} \quad \left \frac{\partial}{\partial x} U(x,t)\right|_{x\in t}\]
\end{document}Output :
In the case of Integral, double limits should be used with the evaluation bar. So, which is shown in the following code.
\documentclass{article}
\begin{document}
\[ \frac{\mathrm{d}}{\mathrm{d} x}\left( \evu{\sin x}{\pi}{x}\right) \]
\[ \evu{\frac{1}{5} \tan \theta}{\pi}{0} \]
\[ \evu{\frac{1}{\ln x}}{a}{b} \quad \evu{\frac{1}{\pi x}}{a_1}{a_2} \]
\end{document}Output :
Use physics package
I created a macro myself in the code above. In the same way, a macro has been defined in the physics package called \eval. Of course, \eval is the best practice for this.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \eval{x}_0^\infty \quad \eval{\frac{1}{e^x \ln x}}_a^b \]
\[ \eval{e^{\sin x}}_{x_1}^{x_2} \]
\[ \eval{\frac{e^x}{2}}^1_0 + 2 \]
\end{document}Output :
Further use of this command is also given below where different brackets have been used on the left side.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \eval(\frac{\sin x}{x}|_0^\infty \]
\[ \eval[\frac{\ln x}{x}|_0^\infty \]
\end{document}Output :