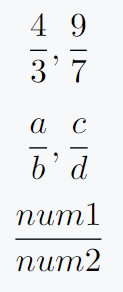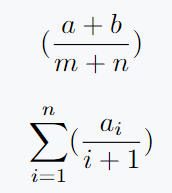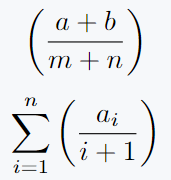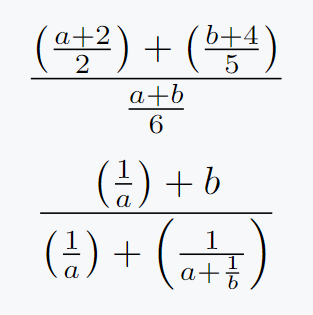In LaTeX, we can use a \frac{arg1}{arg2} command to generate fractions. Fractions are used in mathematical expressions.
Fractions have two parts: numerator, which represents the top of fraction, and denominator, which represents the bottom of fraction.
| Command(Purpose) | frac For fraction operation |
| Mode | Math |
| Package | Default |
| Argument(How much) | YesTwo |
| Syntax | \frac{arg1}{arg2} |
Numerator must be passed in arg1 and denominator in arg2.
Basic example with frac command
The first two examples use simple numerical, but third example uses variables in the numerator and denominator.
\documentclass{article}
\begin{document}
\[ \frac{4}{3}, \frac{9}{7} \]
\[ \frac{a}{b}, \frac{c}{d} \]
\[ \frac{num1}{num2}\]
\end{document}
Output :
Use responsive size bracket with frac
When we do fractions, you will notice its size is very large. If you use brackets in fractions then the size of both will not be adjustable. For example
\documentclass{article}
\begin{document}
\[ (\frac{a+b}{m+n} ) \]
\[ \sum_{i=1}^{n} (\frac{a_i}{i+1})\]
\end{document}
Output :
Look, it doesn’t look responsive at all. If we want to use a responsive bracket, we will use "\left (" and "\right )" commands. Take a look at the example below.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \left(\frac{a+b}{m+n}\right) \]
\[ \sum_{i=1}^{n} \left(\frac{a_i}{i+1}\right)\]
\end{document}
Output :
Nested frac
Nested frac, surely by hearing the name you understand that multiple fracs are used within one frac.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \frac{\left(\frac{a+2}{2}\right)+\left(\frac{b+4}{5}\right)}{\frac{a+b}{6}} \]
\[ \frac{\left(\frac{1}{a}\right)+b}{\left(\frac{1}{a}\right)+\left(\frac{1}{a+\frac{1}{b}}\right)} \]
\end{document}
Output :
Use frac in text
We use a single ‘$’ to enclose \frac command in text.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
Fraction are to represent ratio and division. Thus the fraction $\frac{3}{4}$ can also be used to represent the ratio $3:4$, and the division $3\div4$.\\
The reciprocal of a fraction is another fraction with numerator and denominator exchanged. The reciprocal of $3\div7$, to instance is $7\div3$
\end{document}
Output :