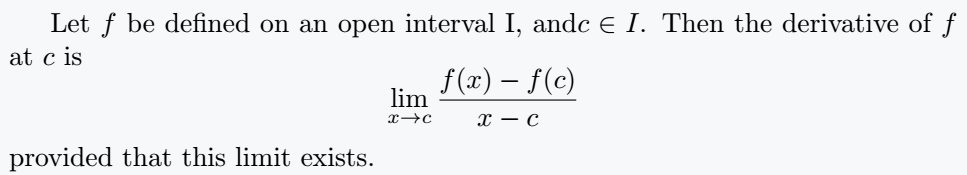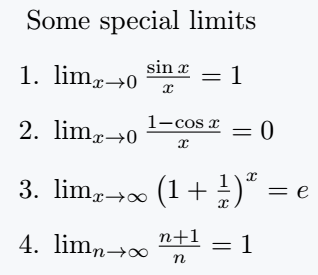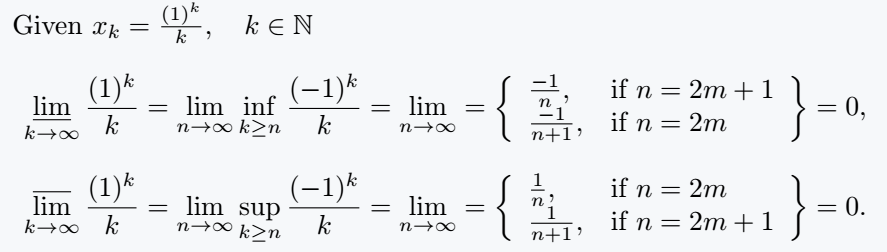How do you write limit(lim) in LaTeX?

The \lim command is used to represent the word lim. However, an arrow and subscript will be required to define the whole syntax.

In this case, there is a to command to represent the “limit arrow”.

The generic LaTeX command for limits is \lim command which displays partial derivative notation lim.

\documentclass{article}
\begin{document}
   A limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Suppose $ f $ is a real-valued function and $ \ell $ is a real number. Intuitively speaking, the expression
   \[\lim _{x \to \ell }f(x)=L  \]
   means that $ f(x) $ can be made to be as close to $ \ell $ as desired, by making $ x $ sufficiently close to $ \ell $
\end{document}

Output :

\[\lim _{x \to 0 }\frac{\sin x}{x}=1 \]

Below is a table showing the various limit commands and their outputs followed by examples demonstrating their usage.

Limits LaTeX commands	Output
\lim	lim
\liminf
\limsup	lim sup
\varinjlim
\varprojlim
\varlimsup
\varliminf
\projlim	proj lim

Other definitions and Demonstrations of limits

\documentclass{article}
\usepackage{amssymb}
\begin{document}
    Let $ (a_n)_{n \in \mathbb{N}} $ be a sequence of real numbers. We define 
    \begin{enumerate}
      \item Limit Superior denoted by $ \limsup  $ 
       \[ \limsup_{n \to \infty} a_n := \lim_{n \to \infty}(\sup\{a_n|k\geq n\}) \]
      \item Limit inferior denoted by $ \liminf  $
       \[ \liminf_{n \to \infty} a_n := \lim_{n \to \infty}(\inf\{a_n|k\geq n\}) \]
     \end{enumerate}
\end{document}

Output :

Other notations for \limsup are \liminf are:

• \varinjlim () corresponds to the direct limit.
  
• \varprojlim () corresponds to the inverse limit. The inverse limit is also known as the projective limit and the LaTeX command for it is \projlim which typesets proj lim.

Examples

Below are some examples using some kind of limit with some mathematical equations, by which you can easily understand it.
Example 1:

\documentclass{article}
\usepackage{amssymb}
\begin{document}
   Let $ f $ be defined on an open interval I, and$  c \in I $. Then the derivative of $ f $ at $ c $ is 
   \[ \lim_{x \to c}\frac{f(x) - f(c)}{x - c} \]
   provided that this limit exists.
\end{document}

Output :

Example 2:

\documentclass{article}
\begin{document}
   Some special limits 
   \begin{enumerate}
    \item $ \lim_{x \to 0}\frac{\sin x}{x} = 1 $ 
    \item $  \lim_{x \to 0}\frac{1 - \cos x}{x} = 0 $ 
    \item $ \lim_{x \to \infty} \left(1  + \frac{1}{x}\right)^x = e  $
    \item $ \lim_{n \to \infty} \frac{n+1}{n} = 1 $
   \end{enumerate}
\end{document}

Output :

Example 3:

\documentclass{article}
\usepackage{amssymb,mathtools}
\begin{document}
   Given $ x_k = \frac{(1)^k}{k}, \quad k \in \mathbb{N}  $
   \[\varliminf_{k \to \infty}  \frac{(1)^k}{k} = \lim_{n \to \infty}\inf_{k \geq n}\frac{(-1)^k}{k} = \lim_{n \to \infty} = \left\{ \begin{array}{ll}
   \frac{-1}{n}, & \text{if $ n = 2m+1 $}\\ 
   \frac{-1}{n+1}, & \text{if $ n = 2m $}
   \end{array}\right\} = 0, \] 
   \[ \varlimsup_{k \to \infty}  \frac{(1)^k}{k} = \lim_{n \to \infty}\sup_{k \geq n}\frac{(-1)^k}{k} = \lim_{n \to \infty} = \left\{ \begin{array}{ll}
   \frac{1}{n}, & \text{if $ n = 2m $}\\ 
   \frac{1}{n+1}, & \text{if $ n = 2m+1 $}
   \end{array}\right\} = 0. \]
\end{document}

Output :

Example 4:

\documentclass{article}
\usepackage{mathtools}
\begin{document}
   Given an inverse system $ ((A_{i})_{i \in I},(f_{ij})_{i\leq j\in I}) $ as a particular subgroup of the direct product of the $ A_{i} $'s, we define the inverse limit(the projective limit)
   \[ A=\varprojlim _{i\in I}{A_{i}}=\projlim _{i\in I}{A_{i}}= \left\{\left.{\vec{a}}\in \prod_{i\in I}A_{i}\;\right|\;a_{i}=f_{ij}(a_{j}){\text{for all }}i\leq j\; {\text{in}}\; I\right\}. \]
   Given a direct system $ \langle A_{i},f_{{ij}}\rangle $, The direct(inductive) limit denoted by  $ \varinjlim A_{i} $ and is defined as 
   \[ \varinjlim A_{i}=\bigsqcup _{i}A_{i}{\bigg /}\sim  \]			
   Its underlying set is the disjoint union of the $ A_{i} $\,'s modulo a certain equivalence relation $ \sim  $
\end{document}

Output :

Conclusion

This web article shows all the uses of Limit. And the table has been created keeping in mind the combination of the types of limits and the output so that you can easily understand it.

Share tutorial