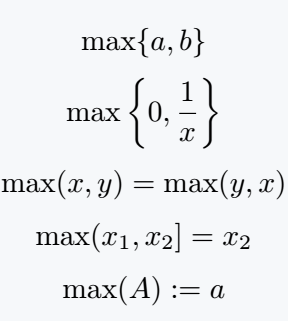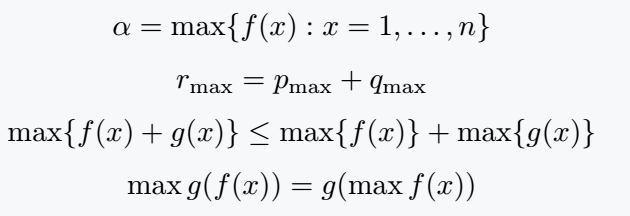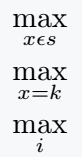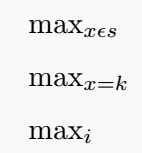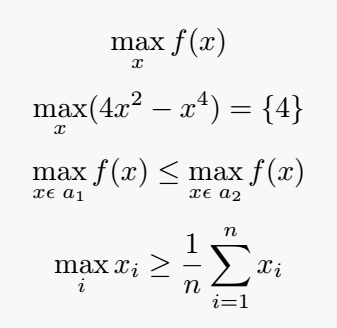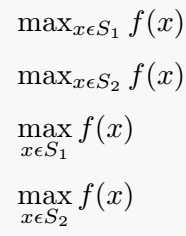How do you write max(a,b) symbol in a LaTeX document?

max function or symbol is printed in a latex document using the default \max command. There are various structural uses of the max function which are nicely explained in this tutorial.

Symbol	Max
Type of symbol	Mathematics
Package	No
Argument	No
Latex command	\max
Example	\max(a,b) → max(a,b)

All kinds of brackets are used when using this symbol or function.

\documentclass{article}
\begin{document}
   $$ \max \{a,b\} $$
   $$ \max \left \{0,\frac{1}{x} \right\} $$
   $$ \max (x,y) = \max (y,x) $$
   $$ \max (x_1,x_2] = x_2 $$
   $$ \max (A):=a $$
\end{document}

Output :

Large expressions are passed in Max. And this symbol is used as subscripted.

\documentclass{article}
\begin{document}
   $$ \alpha = \max \{f(x):x=1,\dots, n\} $$
   $$ r_{\max} = p_{\max} +q_{\max} $$
   $$ \max\{f(x)+g(x)\}\leq \max\{f(x)\}+\max\{g(x)\} $$
   $$ \max g(f(x))=g(\max f(x)) $$
\end{document}

Output :

Subscripted expression with max function in LaTeX

If you use any expression as subscripted with this symbol, it will be at the bottom of the symbol.

\documentclass{article}
\begin{document}
   $$ \max_{x\epsilon s} $$
   $$ \max_{x=k} $$
   $$ \max_i $$
\end{document}

Output :

To get a subscripted expression with Max symbol as output, single dollar should be used instead of double dollar. Which is used for inline math mode.

\documentclass{article}
\begin{document}
   $ \max_{x\epsilon s} $\\[6pt]
   $ \max_{x=k} $\\[6pt]
   $ \max_i $
\end{document}

Output :

LaTeX max over x and logical expression

In this case, you can use the subscript x with the \max command and also use the \limits command before the subscript. Both methods are valid.

\documentclass{article}
\begin{document}
   $$ \max_x f(x) $$
   $$ \max_x(4x^2 - x^4)=\{4\} $$
   $$ \max\limits_{x\epsilon \;a_1} f(x) \leq \max_{x \epsilon \; a_2} f(x) $$
   $$ \max\limits_i x_i \geq \frac{1}{n} \sum\limits^n_{i=1} x_i $$
\end{document}

Output :

If you use inline math mode for text then you must use \limits command. Otherwise, it will remain as a subscript.

\documentclass{article}
\begin{document}
   $ \max_{x\epsilon S_1}f(x) $\\[6pt]
   $ \max_{x\epsilon S_2}f(x) $\\[6pt]
   $ \max\limits_{x\epsilon S_1}f(x) $\\[6pt]
   $ \max\limits_{x\epsilon S_2}f(x) $
\end{document}

Output :