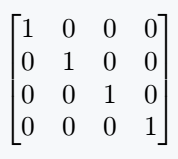
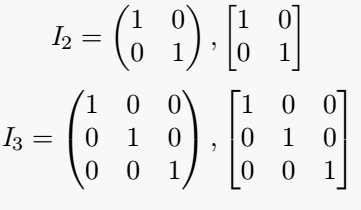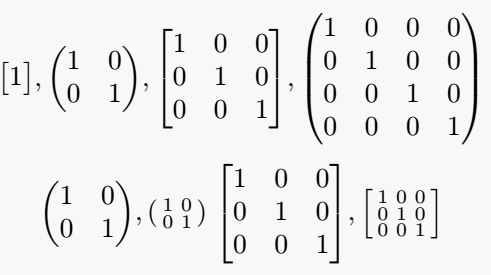In the case of Identity Matrix, digit one is placed in the matrix environment along the diagonal. But, keep in mind that the number of rows and Columns in the environment should be equal.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \begin{bmatrix}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix} \]
\end{document}Output :
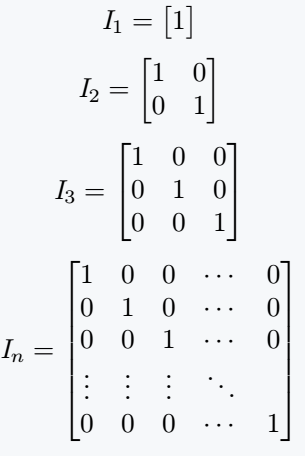
This matrix is denoted by I. And order is used as subscripted with I.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \mathit{I}_1= \begin{bmatrix} 1 \end{bmatrix} \]
\[ \mathit{I}_2= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \]
\[ \mathit{I}_3= \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
\[ \mathit{I}_n= \begin{bmatrix} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots \\ 0 & 0 & 0 & \cdots & 1\end{bmatrix} \]
\end{document}Output :
If you want to keep the matrix elements bound by parenthesis then you have to pass the argument pmatrix in environment.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \mathit{I}_2= \begin{pmatrix} 1 & 0 \\ 0 & 1 \end{pmatrix},\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\]
\[ \mathit{I}_3= \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix},\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
\end{document}Output :
Use physics package for identity matrix
The predefine \imat{n} command will return the identity matrix to you.
However, for brackets and parenthesis, the \imat{n} command must be used as an argument between the \mqty and \smqty commands.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \mqty[\imat{1}], \mqty(\imat{2}), \mqty[\imat{3}],\mqty(\imat{4}) \]
\[ \mqty(\imat{2}), \smqty(\imat{2}) \; \mqty[\imat{3}], \smqty[\imat{3}] \]
\end{document}Output :
For this matrix, the \imat{n} command is very simply represented in the physics package. You just have to use the matrix order as an argument.