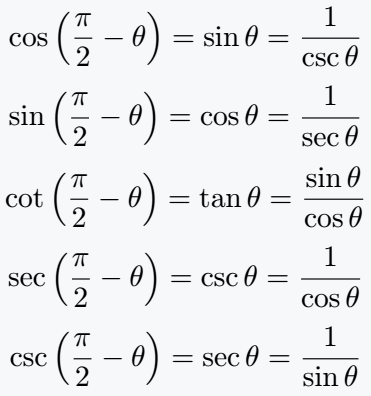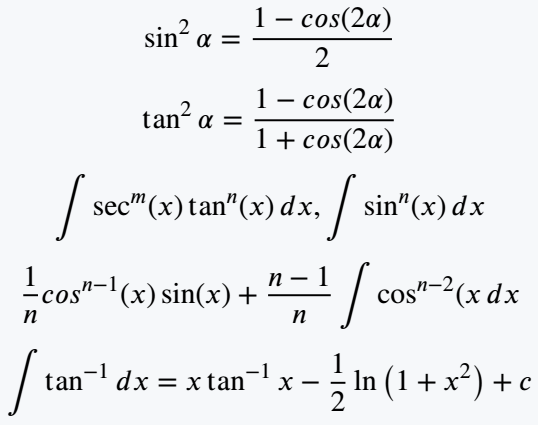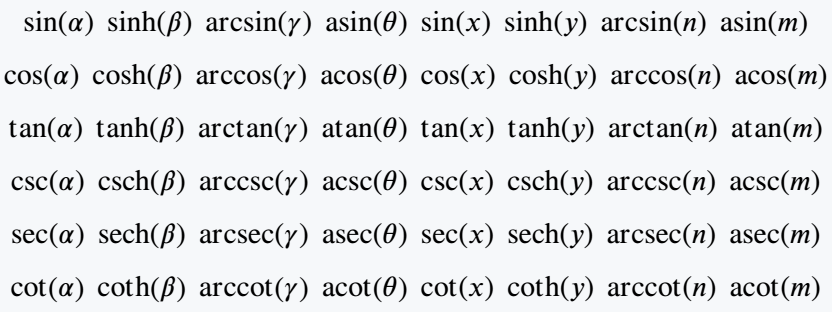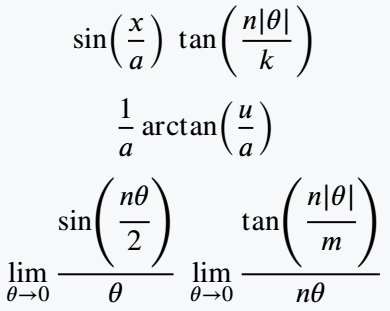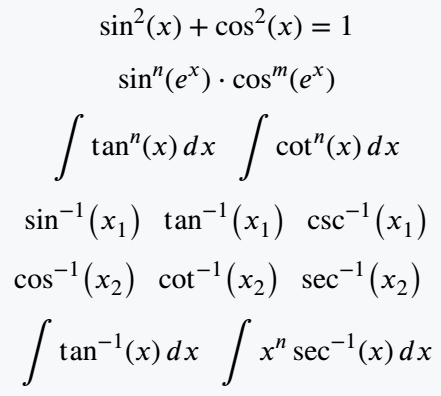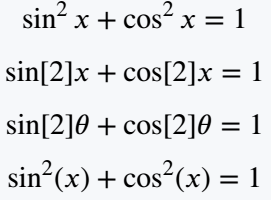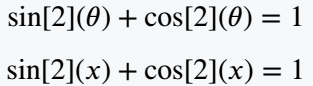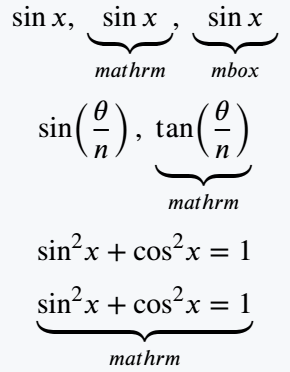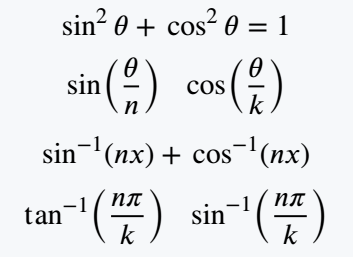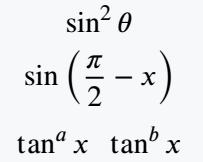From print trigonometry functions to drawing graphs in documents, you can complete every task with the help of LaTeX.
However, in this tutorial, I will discuss in detail how to print math functions or expressions in documents beautifully.
Note the following table where the command is used in the name of the function. For example, \sin for sin.
\documentclass{article}
\begin{document}
\[ \sin(x) \; \sinh(x) \; \arcsin(x) \]
\[ \cos(\theta) \; \cosh(\theta) \; \arccos(\theta) \]
\[ \tan(x) \; \tanh(x) \; \arctan(x) \]
\[ \csc\theta \sec\theta \]
\end{document}Output :
The most commonly used symbol for this function is theta. Of course, there are \theta commands that you know.
But, the theta symbol is not always used with sine, cos, etc. Instead, different expressions are used. And these expressions must be passed in parenthesis as arguments.
If the expression size is comparatively large then the size of parenthesis should be converted to automatically adjustable size by left and right commands.
\documentclass{article}
\begin{document}
\[ \cos\left( \frac{\pi}{2}-\theta \right)= \sin \theta = \frac{1}{\csc\theta} \]
\[ \sin\left( \frac{\pi}{2}-\theta \right)= \cos \theta = \frac{1}{\sec\theta} \]
\[ \cot\left( \frac{\pi}{2}-\theta \right)= \tan \theta = \frac{\sin\theta}{\cos\theta} \]
\[ \sec\left( \frac{\pi}{2}-\theta \right)= \csc \theta = \frac{1}{\cos\theta} \]
\[ \csc\left( \frac{\pi}{2}-\theta \right)= \sec \theta = \frac{1}{\sin\theta} \]
\end{document}Output :
Add power on function in LaTeX
To add power on trigonometry function you need to add it manually. There is no special command for this like physics package where optional arguments are passed as powers.
\documentclass{article}
\begin{document}
\[ \sin^2\alpha = \frac{1-cos(2\alpha)}{2} \]
\[ \tan^2\alpha = \frac{1-cos(2\alpha)}{1+cos(2\alpha)} \]
\[ \int \sec^m(x) \tan^n(x)\,dx, \int \sin^n(x)\,dx \]
\[ \frac{1}{n}cos^{n-1}(x)\sin(x) + \frac{n-1}{n}\int \cos^{n-2}(x\,dx \]
\[ \int\tan^{-1}dx=x\tan^{-1}x-\frac{1}{2}\ln\left(1+x^2\right) +c \]
\end{document}Output :
Use physics package for trigonometric function
So far you have seen use of default command. Now we will take help of external package physics and this package will provide you some features.
First, trigonometry has some functions that don’t have defaults. There are two solutions for this, one of which is using the physics package.
Another solution is to define a new macro for the particular function, as shown last.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \sin(\alpha)\; \sinh(\beta)\;\arcsin(\gamma)\;\asin(\theta)\;\sine(x)\;\hypsine(y)\;\arcsine(n)\;\asine(m)\]
\[ \cos(\alpha)\;\cosh(\beta)\;\arccos(\gamma)\;\acos(\theta)\;\cosine(x)\;\hypcosine(y)\;\arccosine(n)\;\acosine(m) \]
\[ \tan(\alpha)\;\tanh(\beta)\;\arctan(\gamma)\;\atan(\theta)\;\tangent(x)\;\hyptangent(y)\;\arctangent(n)\;\atangent(m) \]
\[ \csc(\alpha)\;\csch(\beta)\;\arccsc(\gamma)\;\acsc(\theta)\;\cosecant(x)\;\hypcosecant(y)\;\arccosecant(n)\;\acosecant(m) \]
\[ \sec(\alpha)\;\sech(\beta)\;\arcsec(\gamma)\;\asec(\theta)\;\secant(x)\;\hypsecant(y)\;\arcsecant(n)\;\asecant(m) \]
\[ \cot(\alpha)\;\coth(\beta)\;\arccot(\gamma)\;\acot(\theta)\;\cotangent(x)\;\hypcotangent(y)\;\arccotangent(n)\;\acotangent(m) \]
\end{document}Output :
Always, it’s not like just using theta or x . So, in this case, the size of parenthesis is automatically adjustable.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \sin(\frac{x}{a})\;\tan(\frac{n|\theta|}{k})\]
\[ \frac{1}{a}\arctan(\frac{u}{a})
\[ \lim_{\theta \to 0}\frac{\sin(\cfrac{n\theta}{2})}{\theta}\;\lim_{\theta \to 0}\frac{\tan(\cfrac{n|\theta|}{m})}{n\theta}\]
\end{document}Output :
Third, is power of trigonometry functions. A separate superscript is not required to obtain in this case.
Optional arguments can be passed along with the command. Inverse trigonometry functions will be easy to define by this method.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \sin[2](x) + \cos[2](x)=1 \]
\[ \sin[n](e^x)\cdot\cos[m](e^x) \]
\[ \int \tan[n](x)\,dx\;\;\int \cot[n](x)\,dx \]
\[ \sin[-1](x_1)\;\;\tan[-1](x_1)\;\;\csc[-1](x_1) \]
\[ \cos[-1](x_2)\;\;\cot[-1](x_2)\;\;\sec[-1](x_2)\;\;\]
\[ \int \tan[-1](x)\,dx \;\; \int x^n \sec[-1](x)\,dx\]
\end{document}Output :
Also noticed a problem with physics package. When you use the optional argument for power, you must include parenthesis.
Because optional arguments will not execute without parenthesis. If you look at the example below.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \sin^{2}x + \cos^{2}x=1 \]
\[ \sin[2]{x} + \cos[2]{x}=1 \] % Without parenthesis
\[ \sin[2]\theta + \cos[2]\theta =1 \] % Without parenthesis
\[ \sin[2](x) + \cos[2](x)=1 \] % With parenthesis
\end{document}Output :
One more thing that isn’t necessary, but good to know. If you want to disable the power option, use notrig as an optional argument when defining physics package.
\documentclass{article}
\usepackage[notrig]{physics}
\begin{document}
\[ \sin[2](\theta) + \cos[2](\theta) =1 \]
\[ \sin[2](x) + \cos[2](x)=1 \]
\end{document}Output :
Use mathrm or mbox commands for math functions
In my opinion, the Coolest feature of LaTeX is defining new commands or redefining existing commands.
Look at the code below and find the difference between each line of output. But, you won’t find any difference.
\documentclass{article}
\usepackage{stix} % for underbrace
\begin{document}
\[ \sin x ,\; \underbrace{\mathrm{sin}\,x}_{mathrm},\; \underbrace{\mbox{sin}\, x}_{mbox} \]
\[ \sin\!\left(\frac{\theta}{n}\right),\; \underbrace{\mathrm{tan}\!\left(\frac{\theta}{n}\right)}_{mathrm} \]
\[ \sin^2\!x + \cos^2 \!x = 1 \]
\[ \underbrace{\mathrm{sin}^2 x + \mathrm{cos}^2 x = 1 }_{mathrm} \]
\end{document}Output :
mathrm or mbox is used behind every default trigonometry command. So, you can define any math function in this way without any commands.
Many math functions do not have a command, but the above method is applicable in all cases.
Create custom command or macro for trig function
No need to write so many expressions again and again. For this, I will create a macro that will be applicable on any math expressions.
All the features should be present like automatic bracket size and power etc.
\fa[power]{fun name}{arg with fun}
\fb[power]{fun name}{arg with fun}
\documentclass{article}
\newcommand{\fa}[3][]{\,\mathrm{#2}^{#1}\,{#3}}
\newcommand{\fb}[3][]{\,\mathrm{#2}^{#1}\!\left( #3 \right)}
\begin{document}
\[ \fa[2]{sin}{\theta} + \fa[2]{cos}{\theta}=1 \]
\[ \fb{sin}{\frac{\theta}{n}}\;\;\fb{cos}{\frac{\theta}{k}} \]
\[ \fb[-1]{sin}{nx} + \fb[-1]{cos}{nx} \]
\[ \fb[-1]{tan}{\frac{n\pi}{k}}\;\;\fb[-1]{sin}{\frac{n\pi}{k}} \]
\end{document}Output :
In case of \newcommand, that name cannot be used, which is used.
\renewcommand is used in exactly the same way. But, in this case, new feature is added to the existing command. For example
\documentclass{article}
\renewcommand{\sin}[2][]{\,\mathrm{sin}^{#1}\,{#2}}
\renewcommand{\tan}[2][]{\,\mathrm{tan}^{#1}\,{#2}}
\begin{document}
\[ \sin[2]{\theta} \]
\[ \sin{\left(\frac{\pi}{2}-x \right)} \]
\[ \tan[a]{x}\;\;\tan[b]{x} \]
\end{document}Output :