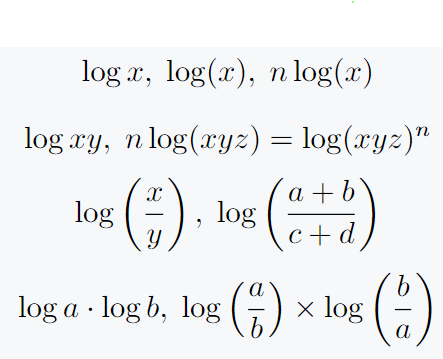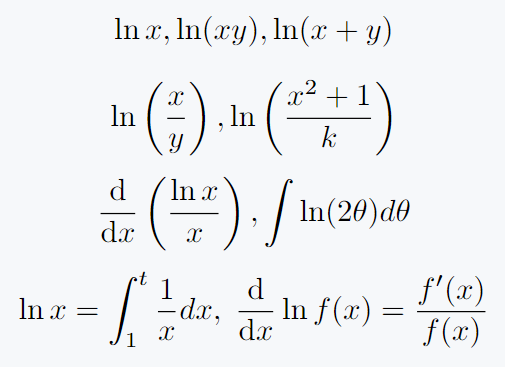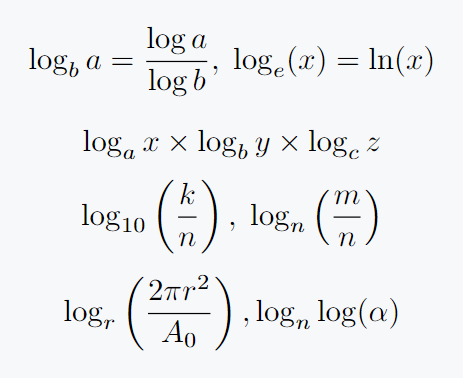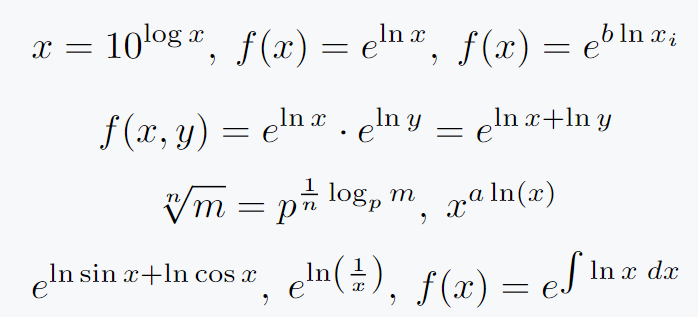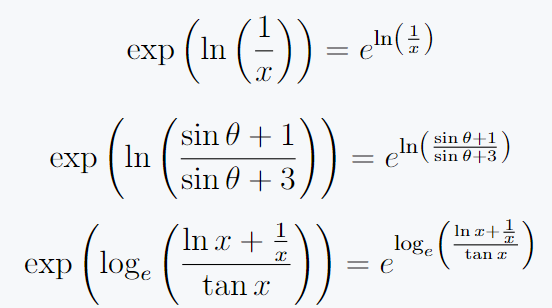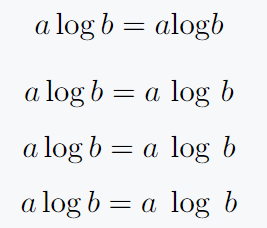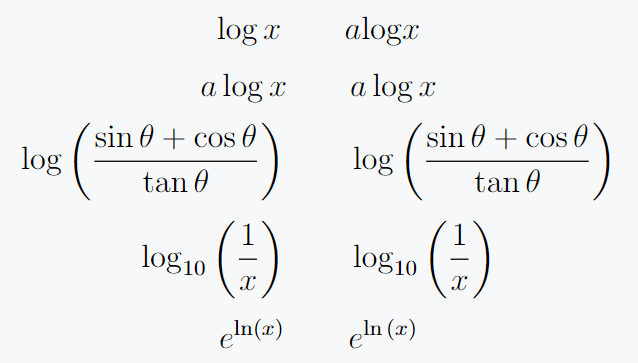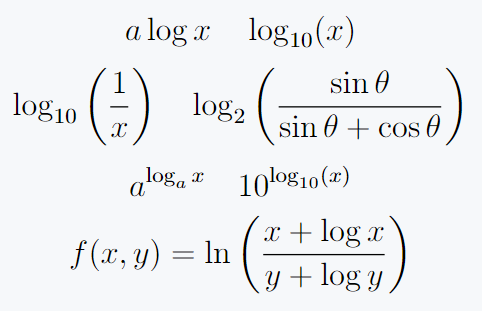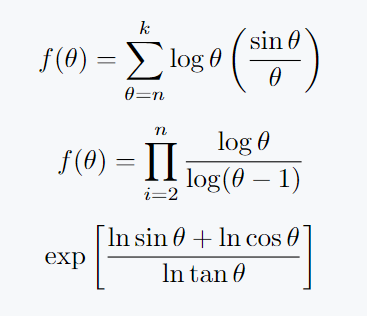Welcome to this tutorial. Instead of a traditional introduction, let’s address the key questions directly.
How can mathematical logarithmic expressions, including natural and base-specific forms, be represented in LaTeX?
How can a custom function be defined without relying on a predefined command?
Additionally, formatting issues, particularly related to spacing, can often arise. This guide provides clear explanations to help you handle them effectively.
To represent arithmetic operators in LaTeX, many commands are predefined. One of them is\log, which represents a normal log. Let’s see the usage below, it will help to understand more.
\documentclass{article}
\begin{document}
\[ \log x , \; \log(x) , \; n\log(x) \]
\[ \log xy , \; n\log(xyz) = \log(xyz)^n \]
\[ \log \left(\frac{x}{y}\right) , \; \log\left(\frac{a+b}{c+d}\right) \]
\[ \log a \cdot \log b , \; \log\left(\frac{a}{b}\right)\times \log\left(\frac{b}{a}\right) \]
\end{document}Output
When using larger expressions with this operator, you need parenthesis, which you add externally.
Natural log function in LaTeX
Similarly, there are \ln default commands for natural log. If you add base e to normal log then refer to ln.
\documentclass{article}
\begin{document}
\[ \ln x, \ln(xy), \ln(x+y) \]
\[ \ln \left(\frac{x}{y}\right), \ln \left(\frac{x^2 + 1}{k}\right) \]
\[ \frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\ln x}{x}\right), \int \ln (2\theta) d\theta \]
\[ \ln x = \int_1^t \frac{1}{x}dx,\; \frac{\mathrm{d}}{\mathrm{d}x} \ln f(x) = \frac{f'(x)}{f(x)} \]
\end{document}Output
Log base functions
Adding base is not a difficult task, if you know the subscript method then you can add easily. Just like adding a subscript, adding a subscript to a \log command will convert to base.
\documentclass{article}
\begin{document}
\[ \log_b a = \frac{\log a}{\log b}, \; \log_e (x) = \ln (x) \]
\[ \log_a x \times \log_b y \times \log_c z \]
\[ \log_{10} \left(\frac{k}{n}\right), \; \log_{n}\left(\frac{m}{n}\right) \]
\[ \log_r \left(\frac{2\pi r^2}{A_0}\right), \log_n\log(\alpha) \]
\end{document}Output
If you add more than one digit or letter to the base, it must be enclosed in curly brackets.
Use log in exp function in LaTeX
When you put a log in an exponential function, you must use log in superscript. Just like subscripts, superscripts are used ^{arg} instead of _{arg}. Let’s see the following example to make the concept more clear.
\documentclass{article}
\begin{document}
\[ x=10^{\log x}, \; f(x) = e^{\ln x}, \; f(x)= e^{b \ln x_i} \]
\[ f(x,y) = e^{\ln x}\cdot e^{\ln y} = e^{\ln x + \ln y} \]
\[ \sqrt[n]{m} =p^{\frac{1}{n}\log_p m}, \; x^{a \ln(x)}\]
\[ e^{\ln \sin x + \ln \cos x}, \; e^{\ln\left(\frac{1}{x}\right)},\; f(x) = e^{\int \ln x\;dx}\]
\end{document}Output
When you use large mathematical expressions with the log function to superscript exponential functions, it is best practice to use \exp functions instead of superscripts.
\documentclass[12pt]{article}
\begin{document}
\[ \exp\left(\ln\left(\frac{1}{x}\right)\right) = e^{\ln\left(\frac{1}{x}\right)} \]
\[ \exp\left(\ln\left(\frac{\sin \theta +1}{\sin \theta + 3}\right)\right) = e^{\ln\left(\frac{\sin \theta +1}{\sin \theta + 3}\right)} \]
\[ \exp\left(\log_e\left(\frac{\ln x + \frac{1}{x}}{\tan x}\right)\right) = e^{\log_e\left(\frac{\ln x + \frac{1}{x}}{\tan x}\right)} \]
\end{document}Output
Add space around function
In LaTeX, proper spacing around mathematical symbols and operators is generally taken care of automatically. However, sometimes you may need to manually adjust the space for various reasons.
Here’s how you can add or modify spacing around the log function or any other command in LaTeX.
\documentclass{article}
\begin{document}
\[ a \log b = a \!\log\!b \]
\[ a \log b = a \,\log\,b \]
\[ a \log b = a \:\log\:b \]
\[ a \log b = a \;\log\;b \]
\end{document}Output
Remember, when making spacing adjustments in LaTeX, it’s crucial to keep readability in mind, ensuring that the final rendered output is clear to readers and doesn’t mislead or cause confusion.
Custom command define
You can define custom commands for the log operator instead of using default commands. If you know the two processes given below, you will know the operator or arithmetic function behind the scenes.
1. Use \mathram command
\mathrm will return you the same font. But, in this case, you have to maintain space. For example
\documentclass{article}
\begin{document}
\[ \log x \qquad a\mathrm{log} x \]
\[ a\log x \qquad a\,\mathrm{log}\, x \]
\[ \log\left( \frac{\sin \theta + \cos \theta}{\tan \theta} \right)\qquad \mathrm{log}\left( \frac{\sin \theta + \cos \theta}{\tan \theta} \right) \]
\[ \log_{10} \left(\frac{1}{x}\right) \qquad \mathrm{log} _{10} \left(\frac{1}{x}\right) \]
\[ e^{\ln (x)} \qquad e^{\mathrm{ln}\,(x)} \]
\end{document}Output
2. Use \DeclareMathOperator from amsmath package
To use \DeclareMathOperator command from amsmath package to create a custom log function, you first need to define the new operator.
This is particularly useful when you want to define a specific type of logarithm or another mathematical operator.
\documentclass[12pt]{article}
\usepackage{amsmath}
\DeclareMathOperator{\logx}{log}
\DeclareMathOperator{\nlog}{ln}
\begin{document}
\[ a\logx x \quad \logx_{10}(x) \]
\[ \logx_{10} \left(\frac{1}{x}\right) \quad \logx_{2}\left(\frac{\sin \theta}{\sin \theta + \cos \theta}\right) \]
\[ a^{\logx_a x} \quad 10^{\logx_{10}(x) }\]
\[ f(x,y)=\nlog \left(\frac{x+ \logx x}{y + \logx y}\right)\]
\end{document}Output
In this example, I’ve defined a new operator named \logx and \nlog that renders as log and ln in the output.
Use physics package for log
The same solution for this mathematical operator is stored in physics package.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[f(\theta)=\sum_{\theta=n}^k \log \theta \left(\frac{\sin \theta}{\theta}\right)\]
\[ f(\theta)= \prod_{i=2}^n \frac{\log \theta}{\log (\theta-1)} \]
\[ \exp \left[ \frac{\ln \sin \theta + \ln \cos \theta}{\ln \tan \theta} \right] \]
\end{document}Output
Conclusion
This tutorial covers all the methods you need. And all kinds of examples are completed, which you constantly deal with in mathematics. If you have any queries after this then feel free to ask.
