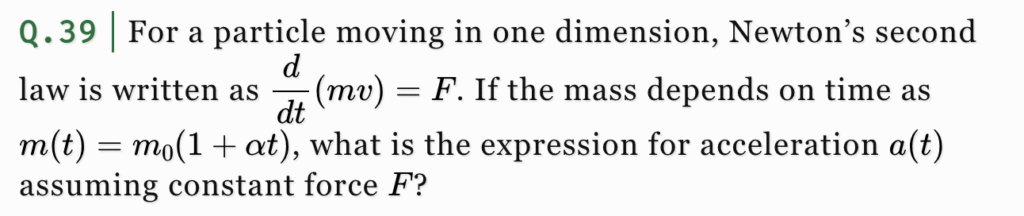Top 46 MCQs on Newton’s Laws of Motion (with Answers)

What does Newton’s First Law state?

1. An object will accelerate if a force is applied
2. An object at rest or in motion will stay in that state unless acted upon by an external force
3. An object always moves in a circle
4. Objects stop moving naturally without force

Explanation

Newton’s First Law, also called the law of inertia, explains that an object will not change its motion unless a force acts on it. Objects at rest stay at rest, and objects in motion stay in motion with constant velocity unless a net external force causes acceleration or deceleration.

What is inertia?

1. The tendency of an object to resist changes in its motion
2. The force that pulls objects toward the Earth
3. The ability of an object to float in water
4. The force required to start a vehicle

Explanation

Inertia is a property of matter that causes objects to resist changes in their state of motion. It depends on the object’s mass—the greater the mass, the greater the inertia.

What is the unit of force in the SI system?

1. Joule
2. Pascal
3. Newton
4. Watt

Explanation

The SI unit of force is the Newton (N), which is defined as the force required to accelerate a one-kilogram mass by one meter per second squared.

According to Newton’s Second Law, force is equal to?

1. Mass + acceleration
2. Mass × acceleration
3. Acceleration ÷ mass
4. Mass ÷ acceleration

Explanation

Newton’s Second Law defines the relationship between force, mass, and acceleration as F = m × a. This means the force acting on an object is the product of its mass and the acceleration it experiences.

What happens to acceleration if the force on an object is doubled but mass remains constant?

1. It is halved
2. It stays the same
3. It is doubled
4. It becomes zero

Explanation

If mass is constant and force is doubled, then acceleration also doubles because force is directly proportional to acceleration.

If the mass of an object is doubled while the force remains constant, what happens to the acceleration?

1. It is halved
2. It stays the same
3. It is doubled
4. It becomes infinite

Explanation

According to F = m × a, if the mass increases while the force remains constant, the acceleration decreases inversely. Doubling the mass halves the acceleration.

What is the direction of the net force relative to acceleration?

1. Always opposite to acceleration
2. At right angles to acceleration
3. In the same direction as acceleration
4. Independent of acceleration

Explanation

The net force on an object is always in the same direction as the acceleration, according to Newton’s Second Law.

What does Newton’s Third Law state?

1. An object’s speed always decreases over time
2. For every action, there is an equal and opposite reaction
3. Objects move in circles when a force is applied
4. Forces act only once and then disappear

Explanation

Newton’s Third Law explains that when one object exerts a force on another, the second object exerts an equal and opposite force back on the first.

If you push a wall, what happens according to Newton’s Third Law?

1. The wall moves in the direction you push
2. The force disappears immediately
3. The wall exerts a greater force than you apply
4. The wall pushes back with equal force in the opposite direction

Explanation

When you push against the wall, the wall applies an equal force back on you in the opposite direction, as described by Newton’s Third Law.

Which quantity is directly related to inertia?

1. Velocity
2. Acceleration
3. Mass
4. Force

Explanation

Inertia depends on the mass of the object. The greater the mass, the more inertia it has, meaning it resists changes in motion more strongly.

When does an object experience balanced forces?

1. When forces are applied in the same direction only
2. When forces cause the object to speed up
3. When all forces acting on the object cancel each other out
4. When friction is greater than applied force

Explanation

Balanced forces occur when the sum of all forces acting on an object is zero, resulting in no change in motion.

What type of force causes an object to slow down?

1. Frictional force
2. Magnetic force
3. Gravitational force
4. Normal force

Explanation

Friction is a resistive force that acts opposite to the direction of motion, causing objects to slow down and eventually stop.

What is the effect of gravity on objects near the Earth’s surface?

1. It repels them away from the Earth
2. It has no effect on moving objects
3. It pulls objects downward toward the Earth’s center
4. It only affects objects in space

Explanation

Gravity is a force that attracts objects toward the Earth’s center, causing them to fall when dropped or influencing their motion near the surface.

Why does a feather fall more slowly than a stone in the absence of air resistance?

1. Because air resistance affects lighter objects more
2. The stone has less mass
3. The feather is affected by magnetic forces
4. The feather floats due to friction alone

Explanation

Air resistance has a greater effect on lighter, larger-surface-area objects like feathers, causing them to fall more slowly compared to denser objects like stones.

What happens if an unbalanced force acts on a stationary object?

1. The object remains at rest
2. The object starts moving in the direction of the force
3. The object moves in a circular path
4. The object disappears

Explanation

An unbalanced force acting on a stationary object causes it to accelerate in the direction of the force, as per Newton’s First and Second Laws.

What is the net force on an object moving with constant velocity?

1. Always equal to gravity
2. Zero
3. Always greater than zero
4. Opposite to acceleration

Explanation

If an object is moving at constant velocity, there is no net force acting on it because all forces are balanced.

Which of the following is an example of Newton’s Third Law?

1. A ball slowing down as it rolls on grass
2. A car gaining speed downhill
3. A swimmer pushing water backward to move forward
4. A rock falling straight down

Explanation

Newton’s Third Law is demonstrated when a swimmer pushes water backward, and the water pushes the swimmer forward with equal force in the opposite direction.

What causes the weight of an object?

1. The object’s speed
2. The object’s temperature
3. The force of gravity acting on the object’s mass
4. The object’s shape

Explanation

The weight of an object is the gravitational force acting on its mass, pulling it toward the Earth.

What happens to an object when all forces are removed in space?

1. It stops immediately
2. It falls toward the nearest planet
3. It continues moving in the same direction at constant speed
4. It spins faster

Explanation

In space, with no external forces like friction or air resistance, an object continues moving in a straight line at constant speed, according to Newton’s First Law.

What determines the acceleration of an object?

1. Only the direction of motion
2. The object’s color
3. The net force and mass of the object
4. The temperature of the environment

Explanation

Acceleration is determined by the net force acting on an object and its mass, as described by Newton’s Second Law.

Why is mass an important factor in motion?

1. It only affects color changes
2. It determines the object’s shape
3. It affects how much force is needed to change the object’s motion
4. It has no effect on motion

Explanation

Mass determines how much inertia an object has and how much force is needed to accelerate it, making it a key factor in motion.

What force opposes motion when two surfaces are in contact?

1. Magnetic force
2. Frictional force
3. Electric force
4. Gravitational force

Explanation

Friction is the force that resists motion between two surfaces in contact, slowing or stopping objects as they move.

How does mass affect inertia?

1. Mass has no relation to inertia
2. Objects with more mass have greater inertia
3. Objects with more mass have less inertia
4. Inertia depends only on shape, not mass

Explanation

Inertia is directly proportional to mass; heavier objects resist changes in motion more than lighter objects.

Which of the following is a vector quantity?

1. Speed
2. Force
3. Distance
4. Time

Explanation

Force is a vector quantity because it has both magnitude and direction, unlike scalar quantities like distance and time.

Why does a spacecraft move forward in space after firing its thrusters?

1. It floats because there is no gravity
2. The expelled gas pushes back on the spacecraft, propelling it forward
3. The thrusters create a magnetic field that attracts it forward
4. Space pulls it in one direction automatically

Explanation

The spacecraft moves forward because of Newton’s Third Law: the gas expelled by the thrusters pushes backward on the spacecraft with equal force, causing it to move forward.

When standing on the ground, what force prevents you from falling through the Earth?

1. Magnetic force
2. Normal force
3. Air resistance
4. Friction only

Explanation

The normal force is the support force exerted by the ground that balances gravity and prevents objects from falling through it.

What happens to the force needed to lift an object as its mass increases?

1. It stays the same
2. It increases
3. It decreases
4. It disappears

Explanation

The heavier an object is, the more force is required to lift it against the force of gravity.

How is acceleration affected if both force and mass are increased proportionally?

1. It remains constant
2. It decreases
3. It increases
4. It becomes zero

Explanation

If both force and mass are increased by the same factor, the acceleration stays constant because the ratio of force to mass remains unchanged.

What force is responsible for keeping planets in orbit around the sun?

1. Gravitational force
2. Frictional force
3. Magnetic force
4. Electric force

Explanation

Gravitational force keeps planets in orbit by constantly pulling them toward the sun while they move forward.

Why can’t you push a wall far?

1. The wall lacks mass
2. There is no force applied
3. The wall exerts an equal and opposite force back on you
4. The wall has no inertia

Explanation

According to Newton’s Third Law, when you apply force to the wall, it pushes back with equal force in the opposite direction, preventing it from moving.

What happens when a net force acts on an object?

1. It always stays at rest
2. It accelerates in the direction of the net force
3. It moves without changing speed
4. It disappears temporarily

Explanation

The object accelerates in the direction of the net force, as described by Newton’s Second Law.

If no net force acts on a moving object, what happens to its motion?

1. It speeds up continuously
2. It keeps moving at constant velocity
3. It stops immediately
4. It reverses direction

Explanation

If no net force acts on the object, it continues moving at a constant velocity because there is nothing to accelerate or decelerate it.

What happens when two objects collide?

1. Only the heavier object exerts force
2. The lighter object absorbs all the force
3. Both objects exert equal and opposite forces on each other
4. No force is exchanged

Explanation

Newton’s Third Law states that during a collision, both objects exert equal and opposite forces on each other, regardless of their mass.

What happens to the motion of a ball if air resistance is ignored?

1. It stops moving quickly
2. It follows a smooth parabolic path
3. It spirals out of control
4. It instantly falls to the ground

Explanation

If air resistance is ignored, the ball’s motion is only affected by gravity and initial velocity, causing it to follow a smooth parabolic trajectory.

What is the effect of friction on a moving object?

1. It accelerates motion
2. It opposes motion and slows it down
3. It makes objects weightless
4. It has no effect on motion

Explanation

Friction opposes the motion of an object by acting in the opposite direction, causing it to slow down or stop.

Which of these is a consequence of Newton’s laws?

1. Objects move randomly without rules
2. Objects respond predictably to forces
3. Forces always disappear after one second
4. All objects eventually stop due to inertia

Explanation

Newton’s laws describe how forces affect the motion of objects in predictable ways, enabling us to understand and calculate their behavior.

A force F is applied to a particle of mass(m), and the motion is described by the equation F = md(v)/dt. If F = kv where k is a constant, what is the form of v(t)?

1. \(\vec{v}(t) = \dfrac{k}{m} t\)
2. \(\vec{v}(t) = \vec{v_0} e^{(k/m)t}\)
3. \(\vec{v}(t) = \vec{v_0} \cos((k/m)t)\)
4. \(\vec{v}(t) = \dfrac{m}{k} (1 – e^{-(k/m)t})\)

Explanation

Given \(\vec{F} = m \dfrac{d\vec{v}}{dt} = k \vec{v}\), rearranging gives \(\dfrac{d\vec{v}}{dt} = \dfrac{k}{m} \vec{v}\). Solving this differential equation yields \(\vec{v}(t) = \vec{v_0} e^{(k/m)t}\).

A block of mass \(m\) slides down a frictionless incline at angle \(\theta\). Which equation correctly gives the acceleration \(a\) along the incline?

1. \(a = g \sin \theta + \mu g \cos \theta\)
2. \(a = g \sin \theta\)
3. \(a = g \cos \theta\)
4. \(a = \dfrac{g}{\sin \theta}\)

Explanation

The only force along the incline is the component of gravity: \(mg \sin \theta\). Newton’s second law yields \(a = \dfrac{mg \sin \theta}{m} = g \sin \theta\).

For a particle moving in one dimension, Newton’s second law is written as \(\dfrac{d}{dt}(m v) = F\). If the mass depends on time as \(m(t) = m_0(1 + \alpha t)\), what is the expression for acceleration \(a(t)\) assuming constant force \(F\)?

1. \(a(t) = \dfrac{F}{m_0}\)
2. \(a(t) = \dfrac{F}{m_0(1 + \alpha t)} – \dfrac{\alpha v(t)}{1 + \alpha t}\)
3. \(a(t) = \dfrac{F}{m_0(1 – \alpha t)}\)
4. \(a(t) = \alpha F t\)

Explanation

Expanding \(\dfrac{d}{dt}(m v)\) gives \(\dfrac{dm}{dt} v + m \dfrac{dv}{dt} = F\). Substituting \(m(t)\) and differentiating, we get \(a(t) = \dfrac{F}{m(t)} – \dfrac{\alpha v(t)}{1 + \alpha t}\).

1. \(a = \dfrac{g(m_1 + m_2)}{m_1 – m_2}\)
2. \(a = \dfrac{g(m_2 – m_1)}{m_1 + m_2}\)
3. \(a = \dfrac{g(m_1 – m_2)}{m_1 + m_2}\)
4. \(a = g \dfrac{m_1 m_2}{m_1 + m_2}\)

Explanation

Applying Newton’s second law to both masses and solving for \(a\), we find \(a = \dfrac{g(m_1 – m_2)}{m_1 + m_2}\).

A force \(\vec{F} = -k\vec{r}\) acts on a particle of mass \(m\). What is the angular frequency \(\omega\) of the resulting motion?

1. \(\omega = \sqrt{\dfrac{k}{m}}\)
2. \(\omega = \dfrac{k}{m}\)
3. \(\omega = \sqrt{k m}\)
4. \(\omega = \dfrac{m}{k}\)

Explanation

The force is a restoring force proportional to displacement, like simple harmonic motion. Newton’s law gives \(m\dfrac{d^2\vec{r}}{dt^2} = -k\vec{r}\), leading to \(\omega = \sqrt{\dfrac{k}{m}}\).

The net force on a particle is given by \(\vec{F} = m \left(\dfrac{d\vec{v}}{dt} + \vec{\omega} \times \vec{v}\right)\). This term \(\vec{\omega} \times \vec{v}\) represents which of the following?

1. Linear drag force
2. Coriolis force in a rotating reference frame
3. Gravitational force variation
4. Electromagnetic force

Explanation

This term appears in rotating frames where \(\vec{\omega}\) is angular velocity and \(\vec{v}\) is velocity. It represents the Coriolis force.

A particle moves under a force given by \(\vec{F} = -b \vec{v}\), where \(b\) is a constant. The equation of motion is \(\dfrac{d\vec{v}}{dt} = -\dfrac{b}{m}\vec{v}\). Which of the following is the correct solution?

1. \(\vec{v}(t) = \vec{v_0} + \dfrac{b}{m}t\)
2. \(\vec{v}(t) = \vec{v_0} \sin(\dfrac{b}{m}t)\)
3. \(\vec{v}(t) = \vec{v_0} e^{-\dfrac{b}{m}t}\)
4. \(\vec{v}(t) = \vec{v_0} e^{\dfrac{b}{m}t}\)

Explanation

The equation is a first-order linear differential equation. Solving yields exponential decay: \(\vec{v}(t) = \vec{v_0} e^{-\dfrac{b}{m}t}\).

The work done by a force \(\vec{F}\) over displacement \(\vec{d}\) is given by \(W = \vec{F} \cdot \vec{d}\). If \(\vec{F} = F_0 (\cos\theta \hat{i} + \sin\theta \hat{j})\) and \(\vec{d} = d_0 \hat{i}\), what is the expression for work?

1. \(W = 0\)
2. \(W = F_0 d_0 \sin\theta\)
3. \(W = F_0 d_0 \cos\theta\)
4. \(W = F_0 d_0\)

Explanation

The dot product gives \(W = F_0 d_0 (\cos\theta \hat{i} \cdot \hat{i} + \sin\theta \hat{j} \cdot \hat{i}) = F_0 d_0 \cos\theta\).

The impulse \(\vec{J}\) is given by \(\vec{J} = \int \vec{F} \, dt\). What is the relationship between impulse and change in momentum \(\Delta \vec{p}\)?

1. \(\vec{J} = \dfrac{\Delta \vec{p}}{2}\)
2. \(\vec{J} = \Delta \vec{p}\)
3. \(\vec{J} = m \vec{v}\)
4. \(\vec{J} = \dfrac{\vec{F}}{\Delta t}\)

Explanation

Impulse is the integral of force over time and equals the change in momentum: \(\vec{J} = \Delta \vec{p}\).

If a particle moves in two dimensions under the force \(\vec{F} = m\vec{a}\), and its acceleration is given by \(\vec{a}(t) = a_0 (\cos(\omega t)\hat{i} + \sin(\omega t)\hat{j})\), what type of motion is this?

1. Circular motion
2. Oscillatory motion along x-axis
3. Free fall motion
4. Random motion

Explanation

The acceleration components describe circular motion in the xy-plane, as the particle accelerates tangentially around a circle.