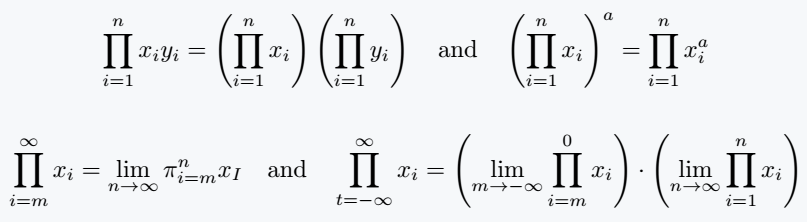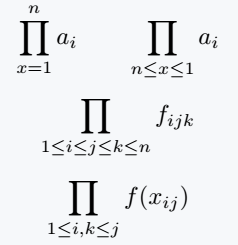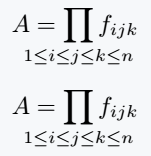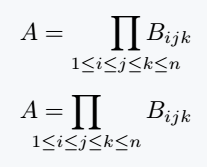How to write product(Π) and big Pi symbol in LaTeX?

In mathematical notation, the product symbol (Π) represents repeated multiplication over a specified range. Unlike the cross (×) symbol, which denotes multiplication between two values, the capital Greek letter Pi (Π) is used for product notation.

LaTeX provides the \prod command to display the this symbol effectively. This guide explores its usage, formatting options, and best practices.

Displaying Product Symbols with Limits

The \prod command in LaTeX allows specifying upper and lower limits using the syntax.

\prod_{min}^{max}

Here, min defines the lower limit, and max sets the upper limit.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
   \[ \prod_{i=1}^{n}x_iy_i = \left(\prod_{i=1}^nx_i\right)\left(\prod_{i=1}^ny_i\right)\quad  \text{and} \quad  \left(\prod_{i=1}^{n}x_i\right)^a = \prod_{i=1}^nx_i^a \]
   \[\prod_{i=m}^{\infty}x_i = \lim_{n \to \infty}\pi_{i=m}^{n}x_I\quad  \text{and}\quad  \prod_{t = -\infty}^{\infty}x_i = \left(\lim_{m \to -\infty}\prod_{i=m}^{0}x_i\right) \cdot \left(\lim_{n \to \infty}\prod_{i=1}^{n}x_i\right) \]
\end{document}

Output :

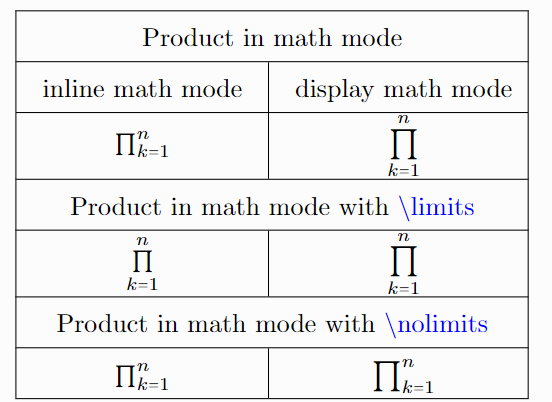
Like integrals and summations, product limits appear differently in inline and display modes. In inline mode, they are placed beside the symbol, while in display mode, they appear above and below.

To control limit placement, use \limits, which forces them above and below in all math modes, or \nolimits, which keeps them next to the symbol.

$Table of \limits and \nolimits for inline and display math mode.$

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  In mathematics, a multiplicative structure is denoted by the capital Pi notation($ \Pi $).\\
    
  Given that $ n \in \mathbb{N}^{\ast} $, the product of n numbers $ x_1,\cdots, x_n $ is denoted $ \prod\limits_{k=1}^nx_k $ and written 
	\[ \prod_{k=1}^nx_k = x_1 \times x_2 \times \cdots \times x_{n-1} \times x_n \]
  The factorial of a number $ n, n \in \mathbb{N}^{\ast} $ using the this notation as 
	\[	n! = \prod\nolimits_{k=1}^nk = 1 \times 2 \times \cdots \times n \quad \text{where}\quad 0! = 1 \]
\end{document}

Output :

Using only a lower limit

LaTeX also allows specifying only a lower limit without an upper bound. When using conditions like ≤, ≥, or = in limits, the notation remains clear and readable.

\documentclass{article}
\begin{document}
   \[ \prod_{x=1}^{n} a_i \qquad \prod_{n\leq x \leq 1} a_i \] 
   \[ \prod_{1\leq i \leq j \leq k \leq n} f_{ijk} \]
   \[ \prod_{1\leq i,k \leq j} f{\left(x_{ij}\right)} \]
\end{document}

Output :

Reducing spacing in long indices

For expressions with long subscripts, spacing may become excessive, affecting readability. LaTeX provides two commands to refine the layout.

1. \smashoperator{} – Reduces unnecessary spacing around operators.
2. \mathclap{} – Compresses the width of large expressions.

\documentclass{article}
\usepackage{mathtools}
\begin{document}
   \[ A = \smashoperator{\prod_{1\leq i \leq j \leq k \leq n}} f_{ijk} \] 
   \[ A = \prod_{\mathclap{1\leq i \leq j \leq k \leq n}} f_{ijk} \]
\end{document}

Output :

The \smashoperator{operator with limits} gives you a possibility to eliminate space either just from the left(l) or right(r). Below is how to achieve that.

\documentclass{article}
\usepackage{mathtools}
\begin{document}
   \[ A = \smashoperator[r]{\prod_{1\leq i \leq j \leq k \leq n}} B_{ijk} \] 
   \[ A = \smashoperator[l]{\prod_{1\leq i \leq j \leq k \leq n}} B_{ijk} \] 
\end{document}

Output :