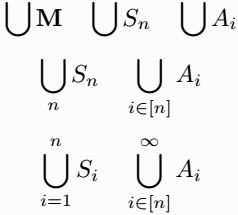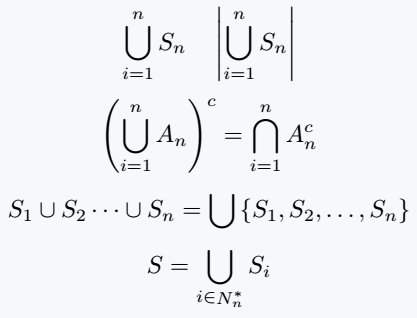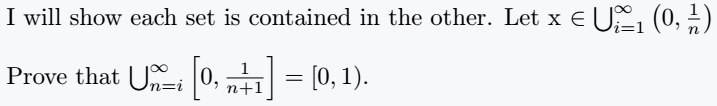Look at the image below, what you are looking for is hidden in this image. Each expression included in this diagram is explained in detail in this tutorial.
You know when and why the big union symbol is used instead of the normal union symbol.
LaTeX has the \bigcup command to render this symbol. Sometimes the lower limit or both limits are used with symbols.
\documentclass{article}
\begin{document}
\[ \bigcup_{i=1}^{n} S_n \quad \left| \bigcup_{i=1}^{n} S_n \right| \]
\[ \left(\bigcup_{i=1}^{n} A_n\right)^c = \bigcap_{i=1}^{n} A_n^c \]
\[ S_1 \cup S_2\cdots \cup S_n =\bigcup\left\{S_1,S_2,\dots,S_n\right\} \]
\[ S = \bigcup_{i \in \mathop N^{*}_{n}}S_i \]
\end{document}Output :
But in the case of inline mode usage is completely different. Due to the reduced vertical space, both limits are on the lighter side vertically and the size of the Big Union is smaller than in math mode.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
I will show each set is contained in the other. Let x $\in \bigcup_{i=1}^\infty\left(0,\frac{1}{n}\right)$\\
Prove that $\bigcup_{n=i}^\infty\left[0,\frac{1}{n+1}\right]=\left[0, 1\right)$.
\end{document}Output :
You can move the limit position completely up and down even in inline mode, but this requires the help of the extra \limits command.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
I will show each set is contained in the other. Let x $\in \bigcup\limits_{n=1}^\infty\left(0,\frac{1}{n}\right)$\\
Prove that $\bigcup\limits_{n=i}^\infty\left[0,\frac{1}{n+1}\right]=\left[0, 1\right)$.
\end{document}Output :
There are also \nolimits commands, which are rarely used. The following table summarizes the concept of limits.