A matrix is an arrangement of numbers, symbols, or expressions in rows and columns.
In LaTeX, writing matrices is simple once you understand their structure.
This tutorial explains step by step how to define matrices, apply different brackets, and even create special matrix types using LaTeX.
Define matrix syntax
To define a matrix, you need to create a proper environment, arrange rows and columns, and insert elements. The amsmath package must be loaded to use these environments.
\begin{matrix}
..... & .... & .... \\
..... & .... & .... \\
..... & .... & ....
\end{matrix}
\begin{matrix} ... \end{matrix}- This environment creates the basic structure for a matrix. You can choose variations like
pmatrixorbmatrixto change the surrounding brackets. &symbol- Separates elements inside a row, helping to organize them into proper columns.
\\command- Moves to the next row in the matrix. Every new row must end with this command.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
\begin{matrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{matrix}
\]
\end{document}Output :
Different types of brackets
LaTeX provides several environments that add different types of brackets around matrices.
Choosing the right one depends on your mathematical notation.
pmatrix |
( ) |
bmatrix |
[ ] |
Bmatrix |
{ } |
vmatrix |
| | |
Vmatrix |
|| || |
Without brackets
If you only need the matrix structure without any enclosing brackets, use the simple matrix environment.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
\begin{matrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{matrix}
\]
\end{document}Output :
Use parentheses
For parentheses around the matrix, replace matrix with pmatrix.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{pmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{pmatrix}\]
\end{document}Output :
Use square brackets
The bmatrix environment is used for square brackets.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{bmatrix}\]
\end{document}Output :
Use curly brackets
For curly brackets, use Bmatrix. Note that case sensitivity matters.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{Bmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{Bmatrix}\]
\end{document}Output :
Use vertical bars
For single vertical bars, apply the vmatrix environment.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[\begin{vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{vmatrix}\]
\end{document}Output :
Use double vertical bars
For double bars, use Vmatrix. Remember the capital V.
\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[ \begin{Vmatrix}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{Vmatrix} \]
\end{document}Output :
Define different types of matrices in LaTeX
You can define special kinds of matrices based on how their elements are arranged.
Square matrix
Rows and columns are equal in size.
\[ \begin{bmatrix}
a_{1,1} & a_{1,2} & \cdots & a_{1,m} \\
a_{2,1} & a_{2,2} & \cdots & a_{2,m} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m,1} & a_{m,2} & \cdots & a_{m,m}
\end{pmatrix} \]Output :
Null matrix
All elements are zero.
\[ \begin{bmatrix}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{bmatrix} \]Output :
Diagonal matrix
Non-zero values appear only on the diagonal.
\[ \begin{bmatrix}
a_{1} & & \\
& \ddots & \\
& & a_{n}
\end{bmatrix} \]Output :
Row matrix
All elements are arranged in a single row.
\[ \begin{pmatrix}
a_{1} & \cdots & a_{n}
\end{pmatrix} \]Output :
Column matrix
All elements are arranged in a single column.
\[ \begin{bmatrix}
a_{1} \\ \vdots \\ a_{n}
\end{bmatrix} \]Output :
Use physics package
Besides amsmath, you can also use the physics package which provides the \mqty command.
\mqty{... & ... \\ ... & ...}
\mqty- This command creates a matrix quickly inside brackets. Rows and columns are separated in the same way using
&and\\. \mqty*- The starred version gives flexibility for adding brackets or bars depending on your notation style.
\documentclass{article}
\usepackage{physics}
\begin{document}
\[ \mqty{a & b \\ c & d} \]
\end{document}Output :
\documentclass{article}
\usepackage{physics}
\begin{document}
\[\mqty{a & b \\ c & d}
\quad
\mqty(a & b \\ c & d)
\quad
\mqty*(a & b \\ c & d)
\quad
\mqty[a & b \\ c & d]
\quad
\mqty|a & b \\ c & d| \]
\end{document}Output :
Best Practice
Use amsmath for standard matrices as it provides clear control over bracket types.
If you need shorthand commands or quick notations, physics with \mqty is very convenient.

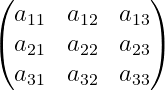
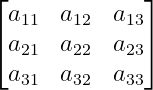
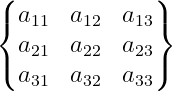
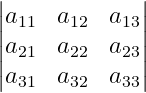
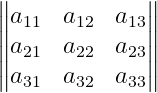
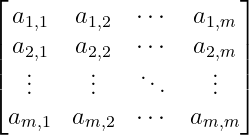
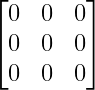
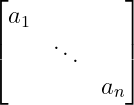
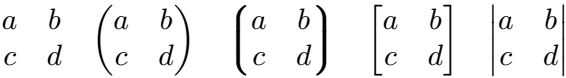
agar hm matrix main matrix k sath numbering dena chahty ho column num or rows ko matrix pa e to wo kaise latix main add ho ga?
kindly plx bta dye.
In the image below, did you want this kind of output? Where the equation number will come with the matrix! Please confirm this ???
