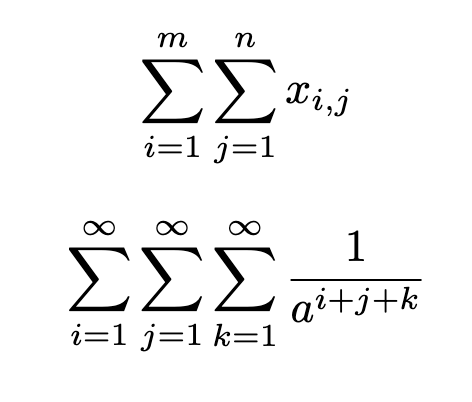Summation in LaTeX Explained with Limits and Multiple Conditions

Summation is one of the most important mathematical notations and is used in algebra, calculus, and statistics.

In LaTeX learners often struggle with how to show limits, how inline and display math behave differently, and how to typeset multiple conditions.

This tutorial explores all the common methods of writing summation in LaTeX with clear syntax and examples.

Summation with subscripts and superscripts

The standard way to write summation in LaTeX is with the command \sum.

Limits are applied using subscripts and superscripts which appear beside the symbol in inline math and above and below in display math.

\sum_{i=1}^{n} a_i

\sum: This command produces the summation symbol and behaves as a large operator that can hold limits.
_{i=1}: This defines the lower bound of the summation. It is placed below the symbol in display math.
^{n}: This defines the upper bound of the summation. It is placed above the symbol in display math.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
   Inline mode: $\sum_{i=1}^{n} i$

   Display mode:
  \[ \sum_{i=1}^{n} i \]
\end{document}

Controlling placement with limits and nolimits

By default LaTeX places limits beside the summation in inline math and above or below in display math.

The commands \limits and \nolimits allow you to override this behavior.

\sum\limits_{i=1}^{n} a_i
\sum\nolimits_{i=1}^{n} a_i

\limits: This forces limits to appear above and below the summation sign even in inline math mode.
\nolimits: This forces limits to stay beside the symbol even in display mode. It overrides the default placement rules.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  With limits: $\sum\limits_{i=1}^{n} i$

  With nolimits: $\sum\nolimits_{i=1}^{n} i$
\end{document}

Double and triple summations

Multiple summations are written by repeating the \sum operator. This is common in multivariable problems.

\sum_{i=1}^{m}\sum_{j=1}^{n} x_{i,j}
\sum_{i=1}^{\infty}\sum_{j=1}^{\infty}\sum_{k=1}^{\infty} \frac{1}{a^{i+j+k}}

\documentclass{article}
\begin{document}
  \[ \sum_{i=1}^{m}\sum_{j=1}^{n} x_{i,j} \]
  \[ \sum_{i=1}^{\infty}\sum_{j=1}^{\infty}\sum_{k=1}^{\infty} \frac{1}{a^{i+j+k}} \]
\end{document}

Multiple conditions under summation

Sometimes multiple conditions are written below the summation.

LaTeX provides several ways to do this such as \atop, \substack, and subarray.

\sum_{i \leq n \atop j \leq n} x_{i,j}
\sum_{\substack{1 \leq i \leq n \\ 1 \leq j \leq n}} x_{i,j}
\sum_{\begin{subarray}{c} 1 \leq i \leq n \\ 1 \leq j \leq n \end{subarray}} x_{i,j}

\atop: This places two conditions under the summation separated by a horizontal divider. It is old TeX style and less flexible.
\substack: This stacks multiple conditions neatly under the summation using line breaks.
subarray: This environment works like substack but gives finer control over alignment of multiple conditions.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  \[ \sum_{\substack{1 \leq i \leq n \\ 1 \leq j \leq n}} x_{i,j} \]
\end{document}

Using sideset for special notation

The \sideset command allows placing symbols or numbers at the corners of the summation sign.

This is useful for primes or extra indices that cannot be handled with normal limits.

\sideset{_{\alpha}^{\beta}}{_{\gamma}^{\sigma}}\sum_{i=1}^{n} x_i
\sideset{}{'}\sum_{i=1}^{n} x_i

\sideset: This command takes two groups of arguments. The first group places symbols on the left side of the operator and the second group places symbols on the right side.

\documentclass{article}
\usepackage{amsmath}
\begin{document}
  \[ \sideset{_{\alpha}^{\beta}}{_{\gamma}^{\sigma}}\sum_{i=1}^{n} x_i \]
  \[ \sideset{}{'}\sum_{i=1}^{n} x_i \]
\end{document}