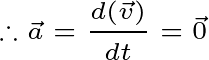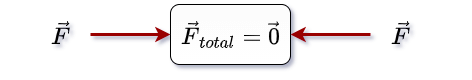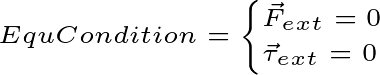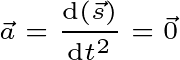In this tutorial, we will discuss an important topic of vectors. Which you call zero vector or null vector. Many people have misconceptions about this zero vector or null vector.
So, I would like to put some examples in front of you before discussing the zero vector in depth.
Suppose the total external force on a particle is zero. And which is in a stable state. Then the total distance of the particle will be
Since the distance of the particle is zero then the displacement of the particle will also be zero. So, then we can write displacement
Many of you will find the above equation to be true. But, the equation written above is meaningless. Because you cannot represent any vector sum by a scalar. You can better understand by looking at the equation above that the displacement is represented by a vector but the zero is represented by a scalar.
So, if you have to write the equation correctly, you have to write zero as a vector. Then which will be the displacement
But you can always describe the absolute value of the vector by a scalar. Then I can write
Then the question may come to your mind what is the difference between scalar zero and vector zero.
Zero-vectors represent those measurable physical quantities that have no specific direction and absolute value.
Zero vector
Simply put, zero vectors are those vectors that have no specific direction and the absolute value is zero.
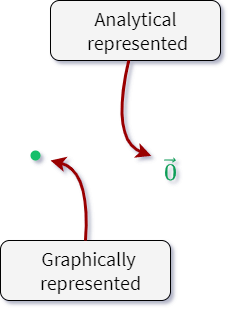
Analytically, all these vectors are denoted by arrow marks above zero. Suppose, here p is zero vector. Then we can write p
And graphically, the zero vector is represented by points. So, look at this figure below
Significance of null Vector
Zero has its existence in reality. But, Zero means nothing. In the same way, the zero vector actually exists but it does not have direction and value.
And in this case, the initial point and the final point are not different but meet at the same point. Thus, the use of vector algebra null vectors is essential.
Practical Application of Zero vector
Here are some real-life examples where zero vectors are used all the time.
Example1 Suppose you went to Los Angeles from California for some work and came back to California in exactly the same way after you finished your work. In this case, if you look at your journey, you will see that your total displacement is zero.
Example2 You are sitting on a train and the train has started moving towards the destination with v speed. With the exception of a few moments, another train has started its journey on your side. When you look at the passengers of the other train, its position seems constant to you.
That is, the relative velocity of the other train will be zero relative to you. For this, you feel constant seeing the position of the passengers of the second train.
And in this case, the velocity of the first train and the velocity of the second train will always be equal.
Example3 Suppose a particle is in equilibrium state. That is, since the particle is moving in space at a constant velocity, the acceleration of the particle will be zero.
Example4 Applying equal force along the horizontal from two opposite sides on an object. In this case, the total applied force on the object is zero. So, look at the figure below so you can understand the concept better.
Then we can write the total applied force as zero-vector.
Example5 Suppose you take a system of n particles. And in this case what will be the total internal force of the system.
If you look at the speed of the system, you will see that according to Newton’s third law, the total internal force of the system will be zero.
Example6 The force is being applied along with the direction in which a particle is moving. At this point, you are asked what is the torque of the particle?
Force is applied in the direction of motion of a particle. In that case, the force cannot convert the linear motion of the particle to rotational motion. And torque is the main cause of rotational motion.
Also, if you look at vector algebra, you will see that there is an important relation between force and torque.
Thus, when the force is applied in the direction of motion of the particle, the angle between the position vector and the force will be zero. Then the total torque of the particle will be
Example7You must have read the equilibrium condition of the system. That is, if the applied external force and torque on a system is zero, the system will be in an equilibrium state. Then we can write external force and torque in the form of zero vector.
In the case of equilibrium condition of system, the acceleration of the system will always be zero.
Example8 Suppose you are moving in a circular path on a bike. And after you hit ten turns on the circular path you were asked “How much is your displacement”?
If you look at your circular motion path, you will see that the initial position and the final position are the same even after hitting ten turns. So, your total displacement will be zero.
Example9 Suppose the equation of the motion of a particle
And if you find the acceleration of a particle using double derivatives of the equation, the acceleration will b
FAQ’s on zero Vector
Question1 What is the difference between zero vector and null vector?
Many of you think that the zero vector and null vector are two different concepts but no. Thus, the zero vector is called the null vector.
Question2 How is the null-vector represented analytically?
The null vector is marked with an arrow above zero.
Question3 How is the null-vector represented graphically?
Graphically null vectors are represented by points
Question4 What is the difference between null vector and unit vector?
Unit vectors have specified values and directions but null vectors have no values and directions. The unit vector always indicates the direction of any vector. However, zero vectors indicate vectors that have no value and no specified direction.
Conclusion
If you have any comments about this tutorial, please let us know in the comments box. If the concept of Zero Vector is clear then you will share this tutorial with your friends.